Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Từ 
= (a / b).8, suy ra:
ab = 8a(b – a)
ab = 8ab – 8a2
8a2 = 7ab
8a = 7b hay 
Giải:
Ta có:
\(\dfrac{a}{b}=\dfrac{-8}{11}\left(1\right)\Leftrightarrow1-\dfrac{a}{b}=1-\dfrac{-8}{11}\)
Hay \(\dfrac{b-a}{b}=\dfrac{11+8}{11}=\dfrac{19}{11}\left(2\right)\)
Thay \(b-a=190\) vào \(\left(2\right)\) ta được:
\(\dfrac{190}{b}=\dfrac{19}{11}\Leftrightarrow190.11=19b\Leftrightarrow b=110\)
Thay \(b=110\) vào \(\left(1\right)\) ta được:
\(\dfrac{a}{110}=\dfrac{-8}{11}\Leftrightarrow11a=-8.110\Leftrightarrow a=-80\)
Vậy phân số \(\dfrac{a}{b}\) cần tìm là \(\dfrac{-80}{110}\)
Thay b - a = 190 vào (1) ta được: 
Phân số a/b phải tìm là -80/110
Gọi phân số lớn nhất cần tìm là a/b
Ta có: 
Theo đề bài thì 8b/15a là số nguyên nên 8b ⋮ 15a
Mà UCLN(8; 15) = 1 và UCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta lại có :
Tương tự 18b ⋮ 35a
Mà UCLN(18: 35) = 1 và UCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra : a ∈ UC(8; 18) = {0,1,2}
b ∈ UC(15; 35) = {0,105; 210; …}
Vì a/b lớn nhất nên a lớn nhất, b nhỏ nhất khác 0
Vậy phân số cần tìm là 2/105
Gọi phân số lớn nhất cần tìm là a/b
Ta có:
Theo đề bài thì 8b/15a là số nguyên nên 8b ⋮ 15a
Mà UCLN(8; 15) = 1 và UCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta lại có :
Tương tự 18b ⋮ 35a
Mà UCLN(18: 35) = 1 và UCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra : a ∈ UC(8; 18) = {0,1,2}
b ∈ UC(15; 35) = {0,105; 210; …}
Vì a/b lớn nhất nên a lớn nhất, b nhỏ nhất khác 0
Vậy phân số cần tìm là 2/105
a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)
Giải:
Ta có:
Do \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{a}< \dfrac{1}{5}\Leftrightarrow a>5\left(1\right)\)
Ta lại có:
\(0< a< b\Leftrightarrow\dfrac{1}{a}>\dfrac{1}{b}\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{a}>\dfrac{1}{a}+\dfrac{1}{b}\)
Hay \(\dfrac{2}{a}>\dfrac{1}{5}\Leftrightarrow\dfrac{2}{a}>\dfrac{2}{10}\Leftrightarrow a< 10\left(2\right)\)
Kết hợp \(\left(1\right)\) và \(\left(2\right)\Leftrightarrow a\in\left\{6;7;8;9\right\}\)
- Với \(a=6\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{1}{30}\Leftrightarrow b=30\)
- Với \(a=7\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{7}=\dfrac{2}{35}\Leftrightarrow b=17,5\) (loại)
- Với \(a=8\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{8}=\dfrac{3}{40}\Leftrightarrow b\approx13,3\) (loại)
- Với \(a=9\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{9}=\dfrac{4}{45}\Leftrightarrow b=11,25\) (loại)
Vậy chỉ có 1 cách viết là \(\dfrac{1}{5}=\dfrac{1}{6}+\dfrac{1}{30}\)
Vì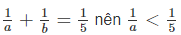 
Suy ra a > 5 (1)
Ta lại có 0 < a < b nên 
Hay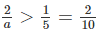 
, suy ra a < 10 (2)
Từ (1) và (2) ta có a ∈ {6;7;8;9}
Nếu a = 6 thì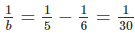 
nên b = 30
Nếu a = 7 thì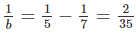 
suy ra b = 17,5 (loại)
Nếu a = 8 thì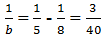 
suy ra b ≈ 13,3 (loại)
Nếu a = 9 thì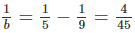 
suy ra b = 11,25 (loại)
Vậy chỉ có một cách viết là 
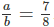
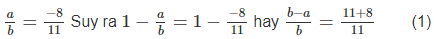
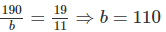
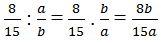
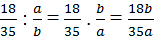
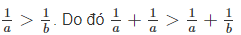
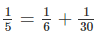
Khi đem mỗi phân số đã cho cộng với phân số \(\dfrac{A}{B}\) thì được hai phân số mới có hiệu không thay đổi và bằng:
\(\dfrac{7}{11}-\dfrac{1}{5}=\dfrac{24}{55}\)
Phân số lớn mới là:
\(\dfrac{24}{55}:\left(3-1\right).3=\dfrac{36}{55}\)
Phân số \(\dfrac{A}{B}=\dfrac{36}{55}-\dfrac{7}{11}=\dfrac{1}{55}\)
Đ/S: \(\dfrac{1}{55}\)