Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

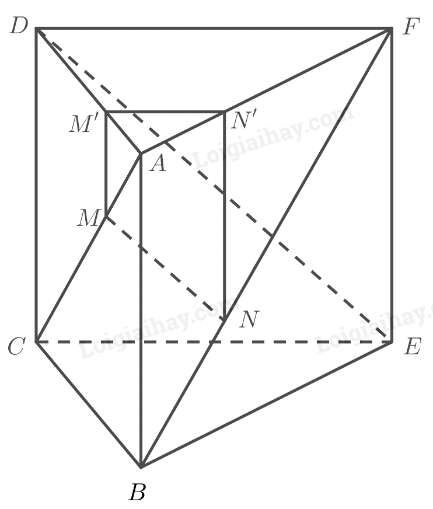
a) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AD\parallel BC\)
Mà \(A{\rm{D}} \subset \left( {ADF} \right)\)
\( \Rightarrow BC\parallel \left( {A{\rm{D}}F} \right)\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AF\parallel BE\)
Mà \(A{\rm{F}} \subset \left( {ADF} \right)\)
\( \Rightarrow BE\parallel \left( {A{\rm{D}}F} \right)\)
Ta có:
\(\left. \begin{array}{l}BC\parallel \left( {A{\rm{D}}F} \right)\\BE\parallel \left( {A{\rm{D}}F} \right)\\BC,BE \subset \left( {CBE} \right)\end{array} \right\} \Rightarrow \left( {CBE} \right)\parallel \left( {A{\rm{D}}F} \right)\)
b) Do \(ABCD\) và \(ABEF\) là hai hình vuông có chung cạnh \(AB\) nên các đường chéo \(AC,BF\) bằng nhau.
Theo đề bài ta có: \(AM = BN\)
\( \Rightarrow \)\(\frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\)
Ta có:
\(MM'\parallel C{\rm{D}} \Rightarrow \frac{{AM}}{{AC}} = \frac{{AM'}}{{A{\rm{D}}}}\)
\(NN'\parallel AB \Rightarrow \frac{{BN}}{{BF}} = \frac{{AN'}}{{AF}}\)
\(\left. \begin{array}{l} \Rightarrow \frac{{AM'}}{{A{\rm{D}}}} = \frac{{AN'}}{{AF}} \Rightarrow M'N'\parallel DF\\M'N' \subset \left( {MNN'M'} \right)\end{array} \right\} \Rightarrow DF\parallel \left( {MNN'M'} \right)\)
\(\left. \begin{array}{l}NN'\parallel EF\\{\rm{NN}}' \subset \left( {MNN'M'} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {MNN'M'} \right)\)
\(\left. \begin{array}{l}DF\parallel \left( {MNN'M'} \right)\\EF\parallel \left( {MNN'M'} \right)\\C{\rm{D}},DF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow \left( {DEF} \right)\parallel \left( {MNN'M'} \right)\)

Nghĩ ra hướng làm rồi cơ mà giờ "bỗng dưng bận" nên để lát nữa tui "múa bút" nhó ahehe :3
Mà viết thử hướng làm cho bà nghĩ coi sao.
Phần bài ũy tích thì sẽ chứng minh theo 2 phần là phần đảo và phần thuận
Phần thuân: Có I là trung điểm MN thì chứng minh khi M, N di động thì I sẽ di động trên đường thẳng HK (H là TD AB, K là trung điểm FC)
Phần đảo: Có I thuộc HK, chứng minh tồn tại 2 điểm M thuộc AC, N thuộc BF sao cho AM=BN và nhận I làm trung điểm MN
Đó, nghĩ thử đi đã :3

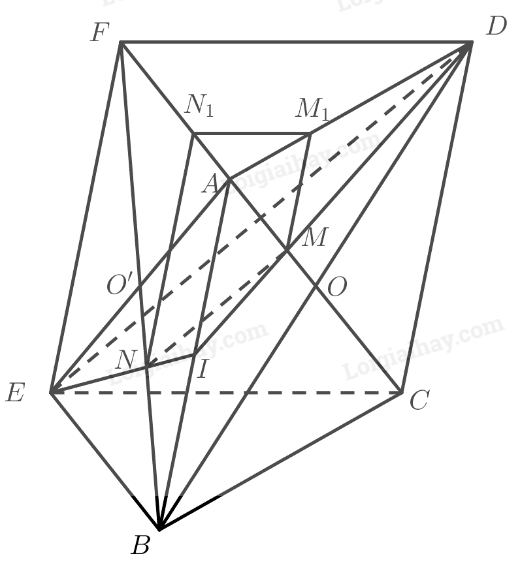
\(\begin{array}{l}\left. \begin{array}{l}N{N_1}\parallel AB \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{BN}}{{BF}} = \frac{1}{3}\\M{M_1}\parallel AB \Rightarrow \frac{{A{M_1}}}{{A{\rm{D}}}} = \frac{{IM}}{{I{\rm{D}}}} = \frac{1}{3}\end{array} \right\} \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{A{M_1}}}{{A{\rm{D}}}}\\\left. \begin{array}{l} \Rightarrow {M_1}{N_1}\parallel DF\\DF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow {M_1}{N_1}\parallel \left( {DEF} \right)\end{array}\)
c) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}N{N_1}\parallel AB\parallel EF\\EF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow N{N_1}\parallel \left( {DEF} \right)\\{M_1}{N_1}\parallel \left( {DEF} \right)\\{M_1}{N_1},N{N_1} \subset \left( {MN{N_1}{M_1}} \right)\end{array} \right\} \Rightarrow \left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\)

a) OO' là đường trung bình của tam giác DBF nên OO' // DF.
DF nằm trong mặt phẳng (ADF) nên OO' // mp(ADF).
Tương tự OO' // CE mà CE nằm trong mặt phẳng (BCE) nên OO' // mp(BCE).
b) Gọi J là trung điểm đoạn thẳng AB, theo định lí Ta-lét \(\Rightarrow\) MN // DE => đpcm.

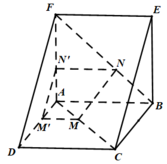
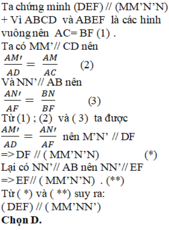
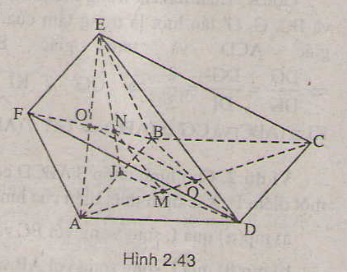



a)
Mà AD, AF ⊂ (ADF)
Nên (ADF) // (BCE)
b) Vì ABCD và ABEF là các hình vuông nên AC = BF. Ta có:
So sánh (1) và (2) ta được:
c) Từ chứng minh trên suy ra DF // (MM′N′N)
Mà DF,EF ⊂ (DEF) nên (DEF) // (MM′N′N)
Vì MN ⊂ (MM′N′N) và (MM′N′N) // (DEF) nên MN // (DEF).