Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{EH}=\overrightarrow{AD},\overrightarrow{FG}=\overrightarrow{AD}\Rightarrow\overrightarrow{EH}=\overrightarrow{FG}\)
=> Tứ giác FEHG là hình bình hành
=> \(\overrightarrow{GH}=\overrightarrow{FE}\) (1)
Ta có \(\overrightarrow{DC}=\overrightarrow{AB},\overrightarrow{AB}=\overrightarrow{FE}\)
=> \(\overrightarrow{DC}=\overrightarrow{FE}\) (2)
Từ (1) và (2) ta có \(\overrightarrow{GH}=\overrightarrow{DC}\)
Vậy tứ giác GHCD là hình bình hành.

A(1;0) B (2;0) C D I(x;x) 4
Từ giả thiết suy ra khoảng cách giữa 2 đường thẳng song song AB, CD bằng 4.
Từ đó, do A, B thuộc Ox nên C(c;4), D(d;4)
Vì 2 đường chéo AC, BD cắt nhau tại I nằm trên đường thẳng y=x nên ta có hệ :
\(\begin{cases}2x=c+1=d+2\\2x=0+4\end{cases}\)
Từ đó tìm được x=2, c=3, d=2.
Vậy C(3;4), D(2;4)
cho mình hỏi hình bình hành có diện tích bằng 4 thì sao suy ra được khoảng cách giữa 2 đường thẳng song song =4

A B C D O M N E F
a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).

Ta có: A là giao điểm của AB và AD. Do đó, tọa độ A là nghiệm của hệ phương trình:
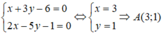
Hình bình hành ABCD có tâm I nên I là trung điểm của AC và BD ⇒ C(-1;3)
Đường thẳng BC đi qua C và song song với AD
Vì BC song song với AD nên BC có dạng: 2x - 5y + c = 0, (c ≠ -1)
Vì C thuộc BC nên: 2.(-1) - 5.3 + c = 0 ⇒ c = 17(tm)
Vậy phương trình đường thẳng BC là: 2x - 5y + 17 = 0
Đường thẳng DC đi qua C và song song với AB
Vì DC song song với AB nên DC có dạng: x + 3y + c = 0, (c ≠ -6)
Vì C thuộc DC nên: -1 + 3.3 + c = 0 ⇒ c = -8(tm)
Vậy phương trình đường thẳng DC là: x + 3y - 8 = 0
