Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

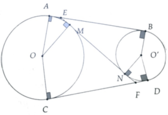
a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF

a: Xét (O) có
MB,MA là các tiếp tuyến
Do đó: MB=MA
Xét (O') có
MA,MC là các tiếp tuyến
Do đó: MA=MC
Ta có: MB=MA
MA=MC
Do đó:MB=MC
=>M là trung điểm của BC
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\left(=BM\right)\)
Do đó: ΔABC vuông tại A
b: ta có: MB=MA
=>M nằm trên đường trung trực của AB(1)
Ta có: OB=OA
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại E
ta có: MA=MC
=>M nằm trên đường trung trực của AC(3)
ta có: O'A=O'C
=>O' nằm trên đường trung trực của AC(4)
từ (3) và (4) suy ra MO' là trung trực của AC
=>MO'\(\perp\)AC tại F
Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật