Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

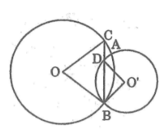
ΔOBC cân tại O nên \(\widehat{BOC}=180^0-2\cdot\widehat{OBC}\)
ΔBO'D cân tại O' nên \(\widehat{BO'D}=180^0-2\cdot\widehat{O'BD}\)
mà \(\widehat{OBC}=\widehat{O'BD}\)
nên \(\widehat{BOC}=\widehat{BO'D}\)

vì C, B cùng thuộc đường tròn (O) => OB=OC => tam giác OBC cân tại O => góc OCB= góc OBC (1)
tương tự góc O'BD= góc O'DB (2)
vì BD là tia pg của góc OBO' => góc OBC= góc DBO' (3)
từ (1) , (2) , (3)=> góc OBC=OCB=O'DB=O'BD
=> góc BOC = góc DO'B

Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
nên OC là phân giác của góc MOA(1) và CM=CA
Xet (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b:
Xét ΔCOD vuông tại O có OM là đường cao
nên MC*MD=OM^2
c: \(AC=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)