Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này hơi khó , bạn tự vẽ hình với làm câu a) nhé 😅😅
b)
00' cắt AB tại H
\(\Rightarrow AH=\frac{AB}{2}=\frac{24}{2}=12\)
Áp đụng Pythagore cho tam giác vuông AOH
\(OH=\sqrt{\left(20^2-12^2\right)}=16\)
Pythagore ▲vuông O'AH Áp dụng Pythagore cho tam giác vuông O'AH
\(O'H=\sqrt{\left(15^2-12^2\right)}=9\)
\(\Rightarrow OO'=OH+O'H=16+9=25cm\)
Vậy : OO' dài 25cm

Gọi I là trung điểm AB. Chú ý 1 A I 2 + 1 O A 2 + 1 O ' A 2
Ta tính được AB=24cm

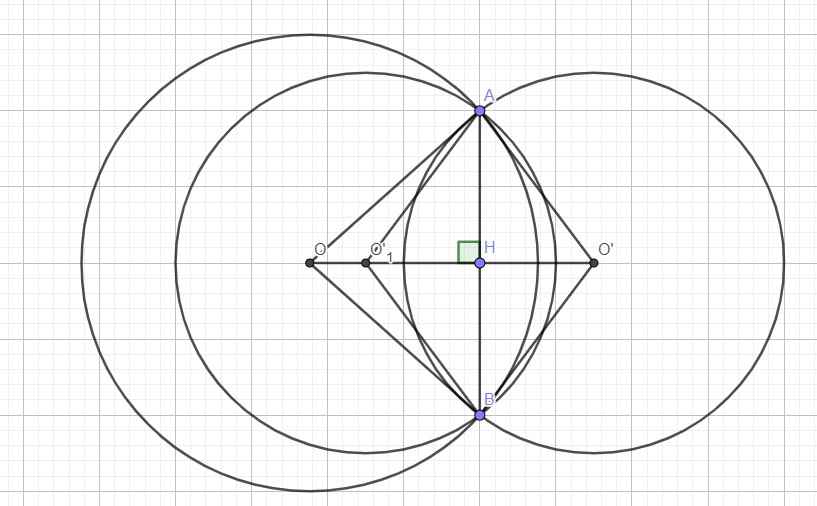
(O) và (O') có 2 vị trí tương đối như hình vẽ, tâm O' có thể nằm ở O' hoặc \(O'_1\)
Gọi H là giao điểm AB và OO', theo tính chất 2 đường tròn cắt nhau ta có H là trung điểm AB và \(OO'\perp AB\)
\(\Rightarrow AH=BH=\dfrac{AB}{2}=4\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông OAH:
\(OH=\sqrt{OA^2-AH^2}=\sqrt{6^2-4^2}=2\sqrt{5}\)
Pitago cho tam giác vuông O'AH:
\(O'H=\sqrt{O'A^2-AH^2}=\sqrt{5^2-4^2}=3\)
\(\Rightarrow\left[{}\begin{matrix}OO'=OH+O'H=2\sqrt{5}+3=7,47\\OO'=OH-O'H=2\sqrt{3}-3=1,47< 2\left(loại\right)\end{matrix}\right.\)

a) Áp dụng định lí Pytago vào ΔABO vuông tại B, ta được:
\(OA^2=OB^2+AB^2\)
\(\Leftrightarrow AB^2=10^2-6^2=64\)
hay AB=8(cm)
b) Xét tứ giác OIBA có
\(\widehat{OIA}=\widehat{OBA}\left(=90^0\right)\)
Do đó: OIBA là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay O,I,B,A cùng thuộc 1 đường tròn
Tâm là trung điểm của OA

a) vuông, nên
Kc là tiếp tuyến, KEF là cát tuyến nên
Suy ra , nên
Ta có nên , từ đó EMOF là tứ giác nội tiếp. (1)
b) Đặt . Ta có ... )uôn nên là ến, KFàcáê u êT c\(DeltaKM\simDetaF.g êtđó O àt gánội ế 1)ặ aó ,nên là tứ iá ộ tip. (2ừ (1) ()y ramđi A , F tộc cng một đường đườgính ủ