Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MB,MA là các tiếp tuyến
Do đó: MB=MA
Xét (O') có
MA,MC là các tiếp tuyến
Do đó: MA=MC
Ta có: MB=MA
MA=MC
Do đó:MB=MC
=>M là trung điểm của BC
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\left(=BM\right)\)
Do đó: ΔABC vuông tại A
b: ta có: MB=MA
=>M nằm trên đường trung trực của AB(1)
Ta có: OB=OA
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại E
ta có: MA=MC
=>M nằm trên đường trung trực của AC(3)
ta có: O'A=O'C
=>O' nằm trên đường trung trực của AC(4)
từ (3) và (4) suy ra MO' là trung trực của AC
=>MO'\(\perp\)AC tại F
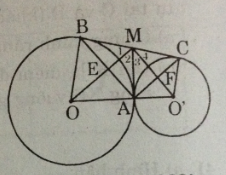
Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật

b)ME.MO = MA2 (hệ thức lượng trong MAO vuông)
MF.MO’ = MA2 (hệ thức lượng trong MAO’ vuông)
Suy ra ME.MO = MF.MO’
c)Đường tròn có đường kính BC có tâm M, bán kính MA.OO’ vuông góc với MA tại A nên là tiếp tuyến của đường tròn (M).
d)Hình b
Gọi I là trung điểm của OO’, I là tâm của đường tròn có đường kính OO’, IM là bán kính (vì MI là trung tuyến ứng với cạnh huyền của MOO’. IM là đường trung bình của hình thang OBCO’ nên IM // OB // O’C. Do đó IM ⊥ BC.
BC vuông góc với IM tại M nên BC là tiếp tuyến của đường tròn (I).

ME.MO = MA2 (hệ thức lượng trong ΔMAO vuông)
MF.MO' = MA2 (hệ thức lượng trong ΔMAO' vuông)
Suy ra ME.MO = MF.MO'

Đường tròn có đường kính BC có tâm M, bán kính MA.OO' vuông góc với MA tại A nên là tiếp tuyến của đường tròn (M).

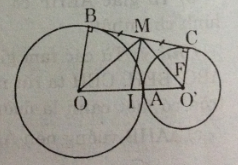
a: Xét (O) có
MA,MB là các tiếp tuyến
nên MA=MB và MO là phân giác của góc BMA(1)
Xét (O') có
MA,MC là các tiếp tuyến
nên MA=MC và MO' là tia phân giác của góc AMC(2)
=>MB=MC
Xét ΔABC có
AM là đường trung tuyến
AM=BC/2
Do đó:ΔABC vuông tại A
b: MB=MA
OB=OA
DO đó: OM là trung trực của AB
=>OM vuông góc với AB
MC=MA
O'A=O'C
DO đó: O'M là đường trung trực của AC
=>O'M vuông góc với AC
Xét tứ giác MEAF có
góc MEA=góc MFA=góc EAF=90 độ
nên MEAF là hình chữ nhật
d: ME*MO=MA^2
MF*MO'=MA^2
DO đó: ME*MO=MF*MO'