Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

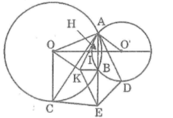
Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3

Gọi B', C' lần lượt là giao điểm khác A của AB, AC với (O').
Do BM, CM là tiếp tuyến của (O') nên ta dễ dàng chứng minh được:
\(BM^2=BA.BB'\); \(CM^2=CA.CC'\)
\(\Rightarrow\dfrac{BM^2}{CM^2}=\dfrac{BA.BB'}{CA.CC'}\). (1)
\(\Delta AOC\sim\Delta AO'C'(g.g)\Rightarrow \frac{AC}{AC'}=\frac{AO}{AO'}\).
Tương tự, \(\frac{AB}{AB'}=\frac{AO}{AO'}\).
Do đó \(\dfrac{AB}{AB'}=\dfrac{AC}{AC'}\Rightarrow\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\Rightarrow\dfrac{AB}{AC}=\dfrac{BB'}{CC'}\). (2)
Từ (1), (2) suy ra \(\dfrac{BM}{CM}=\dfrac{AB}{AC}\).
Theo tính chất đường phân giác đảo thì AM là đường phân giác ngoài của tam giác ABC
\(\Rightarrow\widehat{MAB}+\widehat{MAC}=180^o\Rightarrow180^o+\widehat{BAC}=2\widehat{EAC}\)
\(\Rightarrow180^o-\widehat{EAC}=\dfrac{180^o-\widehat{BAC}}{2}\). (3)
Các tứ giác FDEA, DBAC nội tiếp nên \(\widehat{FDB}=180^o-\widehat{EAC};\widehat{BDC}=180^o-\widehat{BAC}\). (4)
Từ (3), (4) suy ra \(\widehat{FDB}=\dfrac{\widehat{BDC}}{2}\) nên DF là phân giác góc BDC.

a) Ta có: \(\widehat{ANO}=90^0\)
nên N nằm trên đường tròn đường kính AO(1)
Ta có: \(\widehat{AMO}=90^0\)
nên M nằm trên đường tròn đường kính AO(2)
Ta có: \(\widehat{AEO}=90^0\)
nên E nằm trên đường tròn đường kính AO(3)
Từ (1), (2) và (3) suy ra A,M,E,N,O cùng thuộc 1 đường tròn
b) Xét ΔAMK và ΔAIM có
\(\widehat{AKM}=\widehat{AMI}\left(=\dfrac{1}{2}sđ\stackrel\frown{IM}\right)\)
\(\widehat{IAM}\) chung
Do đó: ΔAMK∼ΔAIM(g-g)
Suy ra: \(\dfrac{AM}{AI}=\dfrac{AK}{AM}\)
hay \(AM^2=AK\cdot AI\)

AD là tiếp tuyến của (O)
⇒ \(\widehat{DAB}=\widehat{ACB}\) ( cùng chắn \(\stackrel\frown{AB}\) )
AC là tiếp tuyến của (O)
⇒ \(\widehat{CAB}=\widehat{ADB}\) ( cùng chắn \(\stackrel\frown{AB}\) )
⇒ △ CAB ∼ △ ADB ( g - g )
⇒ \(\dfrac{CB}{AB}=\dfrac{AB}{BD}\Rightarrow AB^2=BC.BD\)

Gọi X và Y lần lượt là giao điểm thứ hai của EM với (O), EN với (O').
Ta có \(\widehat{MAO'}=\widehat{NAO}\left(=90^o\right)\) nên \(\widehat{MAO}=\widehat{NAO'}\). Hơn nữa tam giác MAO và NAO' đều là các tam giác cân nên \(\Rightarrow\widehat{MOA}=\widehat{NO'A}\)
Trong đường tròn (O), ta có: \(\widehat{MOA}=sđ\stackrel\frown{MA}=2.\dfrac{1}{2}sđ\stackrel\frown{MA}=2\widehat{MBA}\)
Tương tự, ta có \(\widehat{NO'A}=2\widehat{ABN}\)
\(\Rightarrow\widehat{MBA}=\widehat{ABN}\)
Hơn nữa có \(\widehat{MAB}=\widehat{ANB}\) (vì chúng lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung nhỏ AB của (O').
\(\Rightarrow\Delta BAM\sim\Delta BNA\left(g.g\right)\)
\(\Rightarrow\dfrac{BA}{BN}=\dfrac{BM}{BA}\)
Do \(BA=BE\) nên \(\dfrac{BE}{BN}=\dfrac{BM}{BE}\)
Lại có \(\widehat{MBA}=\widehat{ABN}\left(cmt\right)\) \(\Rightarrow\widehat{EBM}=\widehat{EBN}\)
\(\Rightarrow\Delta MBE\sim\Delta EBN\left(c.g.c\right)\)
\(\Rightarrow\widehat{MEB}=\widehat{ENB}\)
Lại có \(\widehat{ENB}=\widehat{BNY}=\widehat{BAY}\) nên \(\widehat{MEB}=\widehat{BAY}\) \(\Rightarrow\) EX//AY
\(\Rightarrow\widehat{AYN}=\widehat{MEN}\)
Hơn nữa vì \(\widehat{NAx}=\widehat{AYN}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung nhỏ AN trong (O'))
\(\Rightarrow\widehat{NAx}=\widehat{MEN}\)
Từ đó suy ra tứ giác AMEN nội tiếp (góc ngoài bằng góc trong đối)
Ta có đpcm.