Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

Gọi A, B, C lần lượt là chân đường vuông góc kẻ từ I đến a, b, c.
Xét hai góc trong cùng phía E và F.
Do I thuộc tia phân giác của góc E nên IA = IC(1)
Do I thuộc tia phân giác của góc F nên IC = IB(2)
Từ (1) và (2) suy ra IA = IB = IC
hay I cách đều ba đường thẳng a, b, c.

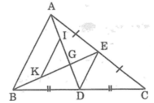
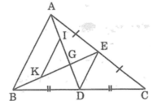
Vì AD và BE là 2 đường trung tuyến của ΔABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 2/3 AD

Áp dụng kết quả bài 64 chương II sách Bài tập toán 7 vào ΔABC và ΔAGB ta có:
DE // AB và DE = 1/2 AB (1)
IK // AB và IK = 1/2 AB (2)
Từ (1) và (2) suy ra:
DE // IK và DE = IK.
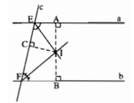

Gọi A, B, C lần lượt là chân đường vuông góc kẻ từ I đến a, b, c. Xét hai góc trong cùng phía E và F. Do I thuộc tia phân giác của góc E nên IA = IC. (1)
Do I thuộc tia phân giác của góc F nên IC = IB. (2)
Từ (1) và (2) suy ra IA = IB = IC, tức là I cách đều ba đường thẳng a, b, c.