Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Chọn D
TH1:
Ta có Đ O : M x ; y → M ' ( x ' ; y ' ) . Khi đó: x ' = − x y ' = − y ⇔ x = − x ' y = − y '
Từ x + y − 2 = 0 ⇔ − x ' − y ' − 2 = 0
Vậy có ảnh d 1 : x + y + 2 = 0 .
Tiếp tục qua phép tịnh tiến v → = 3,2 có T v → : N x ; y → N ' x ' ; y ' khi đó x ' = x + 3 y ' = y + 2 ⇔ x = 3 − x ' y = 2 − y ' .
x + y + 2 = 0 ⇔ 3 − x ' + 2 − y ' + 2 = 0 ⇔ 7 − x ' − y ' = 0
Vậy ảnh là d ' : x + y − 7 = 0 .
TH2:
Ta có qua phép tịnh tiến v → = 3,2 có T v → : N x ; y → N ' x ' ; y ' khi đó x ' = x + 3 y ' = y + 2 ⇔ x = 3 − x ' y = 2 − y ' . Từ x + y − 2 = 0 ⇔ 3 − x ' + 2 − y ' − 2 = 0 ⇔ 3 − x ' − y ' = 0
Vậy có ảnh d 1 : x + y − 3 = 0 .
Tiếp tục Đ O : M x ; y → M ' ( x ' ; y ' ) . Khi đó: x ' = − x y ' = − y ⇔ x = − x ' y = − y '
Từ x + y − 3 = 0 ⇔ − x ' − y ' − 3 = 0
Vậy ảnh là d ' : x + y + 3 = 0 .

\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra

Đáp án C
Các phép biến hình luôn biến 1 đường thẳng thành 1 đường thẳng song song hoặc trùng với nó là: Tịnh tiến, đối xứng tâm, phép vị tự.

Đáp án là D
Có vô số phép tịnh tiến biến một đường thẳng thành chính nó. Đó là các phép tịnh tiến có véc tơ tịnh tiến là véc tơ không hoặc véc tơ tịnh tiến là véc tơ chỉ phương của đường thẳng đó.

Đáp án C
Độ dài bé nhất của vecto u → bằng khoảng cách từ một điểm bất kì trên d tới d’ bằng
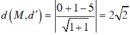

Chọn đáp án A.
Phép tịnh tiến theo v → biến đường thẳng d thành chính nó khi vectơ v → cùng phương với vectơ chỉ phương của d. Mà d có VTCP v → = 2 ; 4 .

Đáp án D