Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy điểm O tuỳ ý.
Qua O vẽ 9 đường thẳng lần lượt song song với 9 đường thẳng đã cho. 9 đường thẳng qua O tạo thành 18 góc không có điểm trong chung, mỗi góc này tương ứng bằng góc giữa hai đường thẳng trong số 9 đương thẳng đã cho.
Tổng số đo của 18 góc đỉnh O là 3600 do đó ít nhất có 1 góc không nhỏ hơn 3600 : 18 = 200 , từ đó suy ra ít nhất cũng có hai đường thẳng mà góc nhọn giữa chúng không nhỏ hơn 200 .
mk chỉ bít
Cho 9 đường thẳng trong đó không có hai đường thẳng nào song song. Chứng minh rằng cũng có hai đường thẳng mà góc nhọn giữa chúng không nhỏ hơn 20

Hướng dẫn:
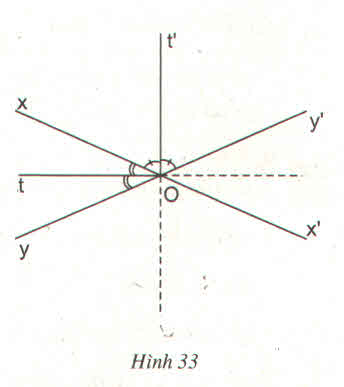
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ + ˆxOy′xOy′^)
mà (ˆxOyxOy^ + ˆxOy′xOy′^) = 1800 (2 góc kề bù)
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 12121800 = 900
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của ˆxOyxOy^ nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của ˆxOy′xOy′^ nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc ˆxOyxOy^, ˆxOy′xOy′^, ˆx′Oy′x′Oy′^, ˆx′Oyx′Oy^ thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ +

mik biet moi i a) và b) thui
a) xét tam giác AOM và tam giác BOM ta có :
OA = OB ( GIẢ THIẾT )
góc AOM = góc MOB
OM là cạnh chung
=> tam giác AOM = tam giác BOM
b) từ a) => am = bm

Ta có hình vẽ:
O x y t A B M N
a/ Xét tam giác OBM và tam giác OAM có:
OM: chung
MOA = MOB (GT)
OA = OB (GT)
=> tam giác OBM = tam giác OAM (c.g.c)
b/ Ta có: tam giác OAM = tam giác OBM
=> AM = BM (2 cạnh tương ứng)
Ta có: tam giác OAM = tam giác OBM
=> góc OMA = góc OMB (2 góc tương ứng)
Mà góc OMA + góc OMB = 1800
=> góc OMA = góc OMB = 1800:2=900
Vậy OM \(\perp\)AB (đpcm)
c/ Vì OM \(\perp\)AB
và AM = BM
=> OM là trung trực của AB (đpcm)
d/ Xét tam giác ONA và tam giác ONB có:
góc NOA = góc NOB (GT)
ON: cạnh chung
OA = OB (GT)
=> tam giác ONA = tam giác ONB (c.g.c)
=> NA = NB (2 cạnh tương ứng)
a) Xét t/g OBM và t/g OAM có:
OB = OA (gt)
BOM = AOM (gt)
OM là cạnh chung
Do đó, t/g OBM = t/g OAM (c.g.c) (đpcm)
b) t/g OBM = t/g OAM (câu a)
=>BM = AM (2 cạnh tương ứng) (1)
OMB = OMA (2 góc tương ứng)
Mà OMB + OMA = 180o ( kề bù)
Nên OMB = OMA = 90o
=> OM _|_ AB (2)
(1) và (2) là đpcm
c) Có: AM = BM (câu b)
Mà OM _|_ AB (câu b) => OM là đường trung trực của AB (đpcm)
d) C/m tương tự câu a ta cũng có: t/g AON = t/g BON (c.g.c)
=> NA = NB (2 cạnh tương ứng) (đpcm)

a) Từ A kẻ A m / / b (Am nằm trong a O b ^ )
Kẻ tia Ay là tia phân giác của a A m ^ .
Ta có: a O t ^ = 1 2 a O b ^ (Ot là tia phân giác của a O b ^ )
a A y ^ = 1 2 a A m ^ (Ay là tia phân giác của a A m ^ )
Mà a O b ^ = a A m ^ (hai góc đồng vị) ⇒ a O t ^ = a A y ^
Hai góc này lại ở vị trí đồng vị nên A y / / O t
b) Vẽ tia A z ⊥ A y
Lại có A y / / O t (theo phần a)
⇒ A z ⊥ O t (Az vuông góc với một trong hai đường thẳng song song thì phải vuông góc với đường thẳng còn lại).