Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AB không song song với d nên AB cắt d tại N
Với \(M\in d\) thì ta có ΔMAB
Xét ΔMAB có |MA-MB|<AB
Nếu M trùng với N thì |MA-MB|=AB
=>Để |MA-MB| lớn nhất thì M trùng với N

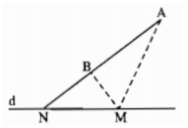
Vì AB không song song với d nên AB cắt d tại N.
Với điểm M bất kỳ thuộc d mà M không trùng với N thì ta có tam giác MAB.
Theo hệ quả bất đẳng thức tam giác ta có:
|MA−MB| < AB
Khi M ≡ N thì
|MA−MB|= AB
Vậy |MA−MB| lớn nhất là bằng AB, khi đó M ≡ N là giao điểm của hai đường thẳng d và AB.

Mọi người làm nhanh jup mik nhé, ai có đáp án sẽ k luôn. Kamsa =)

Ta có: \(\left|MA-MB\right|\ge0\) với một điểm M tùy ý.
\(\left|MA-MB\right|=0\) chỉ với điểm M mà MA = MB
=> M nằm trên đường trung trực của đoạn thẳng AB. (Có giao điểm này vì AB không vuông góc với đường thẳng d)
Vậy, \(\left|MA-MB\right|\) đạt GTNN là 0 khi M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB.

BH vuong goc voi AM=>BH=<BM
CE vuong goc voi AM=>CE=<CM
=>BH+CE=<BM+CM
=>d=<BC
Dau bang xay ra khi BH=BM; CE=CM
=>AM vuong goc voi BC
Vì điểm M cách đều hai điểm A và B nên M thuộc đường trung trực của đoạn thẳng AB.
Vậy điểm M là giao điểm của đường thẳng d với đường trung trực của AB.