Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

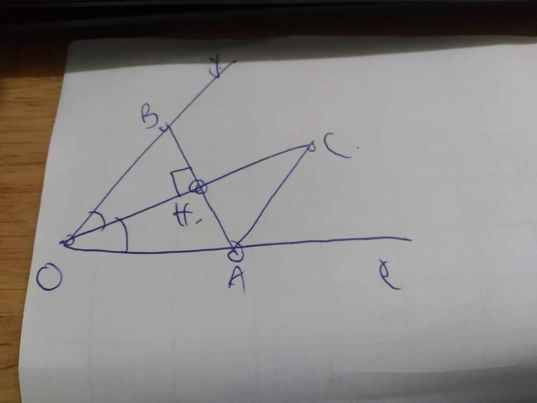
b: Xét ΔOBA có
OH là đường cao
OH là đường phân giác
Do đó: ΔOBA cân tại O
=>OB=OA
Ta có: ΔOBA cân tại O
mà OH là đường cao
nên H là trung điểm của AB
Xét ΔHCA vuông tại H và ΔHOB vuông tại H có
HA=HB
\(\widehat{HAC}=\widehat{HBO}\)(hai góc so le trong, AC//OB)
Do đó: ΔHCA=ΔHOB
=>HC=HO
=>H là trung điểm của OC
Xét ΔAOC có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔAOC cân tại A
=>AC=AO

a: Xét ΔOHA vuông tại H và ΔOHB vuông tại H có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
=>OA=OB
b: Điểm D ở đâu vậy bạn?

a: Xét ΔMOA vuông tại M và ΔMOB vuông tại M có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔMOA=ΔMOB
Suy ra: OA=OB
b: Ta có: ΔMOA=ΔMOB
nên AM=BM
Xét ΔEMA vuông tại M và ΔEMB vuông tại M có
EM chung
AM=BM
Do đó: ΔEMA=ΔEMB
Suy ra: \(\widehat{AEM}=\widehat{BEM}\)
hay EM là tia phân giác của \(\widehat{AEB}\)