Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) xét tam giác AOM và tam giác BOM
Có: OM : cạnh huyền
góc BOM =AOM
=>tam giác BOM =tam giác AOM (cạnh huyền -góc nhọn)
=> OA =OB ( 2 cạnh tương ứng )
c)Ta có tam giác AOM=BOM (câu a)
=>MA=MB
Vậy OM là đường trung trực của AB

a) ∆AOH và ∆BOH có:
ˆAOH=ˆBOH (gt) OH là cạnh chung
∆AOH =∆BOH( g.c.g)
Vậy OA=OB.
b) ∆AOC và ∆BOC có:
OA=OB (cmt)
ˆOAC = ˆOAB (gt)
OC cạnh chung.
Nên ∆AOC= ∆BOC(g.c.g)
Suy ra: CA=CB (hai cạnh tương ứng)
ˆOAC= ˆOBC ( góc tương ứng).

a) ∆AOH và ∆BOH có:=
(gt)
OH là cạnh chung
∆AOH =∆BOH( g.c.g)
Vậy OA=OB.
b) ∆AOC và ∆BOC có:
OA=OB(cmt)
=
(gt)
OC cạnh chung.
Nên ∆AOC= ∆BOC(g.c.g)
Suy ra: CA=CB(cạnh tương ứng)
=
( góc tương ứng).

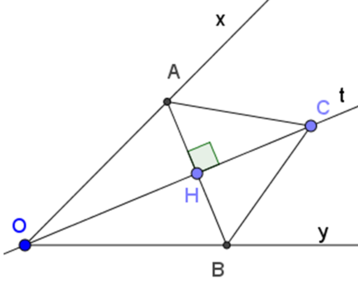
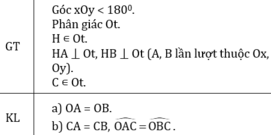
ΔAOH và ΔBOH có
∠ AOH = ∠ BOH (vì Ot là tia phân giác góc xOy)
OH cạnh chung
∠ OHA = ∠ OHB (= 90º)
⇒ ΔAOH = ΔBOH (g.c.g)
⇒ OA = OB (hai cạnh tương ứng)

A B C H O x y t 1 2
a)
xét \(\Delta AHO\) và \(\Delta BHO\) có:
OH(chung)
\(\widehat{AHO}=\widehat{BHO}=90^o\)
\(\widehat{O_1}=\widehat{O_2}\left(gt\right)\)
\(\Rightarrow\Delta AHO=\Delta BHO\left(g.c.g\right)\)
=> OA=OB
b)
xét \(\Delta ACO\) và \(\Delta BCO\) có:
OA=OB(theo câu a)
\(\widehat{O_1}=\widehat{O_2}\)(gt)
OC(chung)
=>\(\Delta ACO=\Delta ABO\left(c.g.c\right)\)
=>\(\begin{cases}\widehat{OAC}=\widehat{OBC}\\CA=CB\end{cases}\)

tự vẽ hình
a) Xét \(\Delta\)HAO vuông tại H và \(\Delta\)HBO vuông tại H
có : OH chung ; gócHOA =gócHOB ( Ot : phân giác)
=> \(\Delta\)HAO =\(\Delta\)HBO ( cạnh góc vuông - góc nhọn)
=> OA =OB ( cạnh tương ứng)
b) Xét \(\Delta\)CAO và \(\Delta\)CBO
có OA =OB ( cm trên)
gócCOA =góc COB
OC chung
=>\(\Delta\)CAO =\(\Delta\)CBO ( c-g-c)
=> góc OAC = góc OBC ( góc tương ứng)

a) ∆AOH và ∆BOH có:ˆAOHAOH^=ˆBOHBOH^(gt)
OH là cạnh chung
∆AOH =∆BOH( g.c.g)
Vậy OA=OB.
b) ∆AOC và ∆BOC có:
OA=OB(cmt)
ˆOACOAC^=ˆOABOAB^(gt)
OC cạnh chung.
Nên ∆AOC= ∆BOC(g.c.g)
Suy ra: CA=CB(cạnh tương ứng)
ˆOACOAC^= ˆOBCOBC^( góc tương ứng).
Xem thêm tại: http://loigiaihay.com/bai-35-trang-123-sach-giao-khoa-toan-7-tap-1-c42a5064.html#ixzz48jIcx
a) Xét ΔAOH∆AOH và ΔBOH∆BOH có:
+) ˆAOH=ˆBOHAOH^=BOH^ (vì OtOt là phân giác)
+) OHOH là cạnh chung
+) ˆAHO=ˆBHO(=900)AHO^=BHO^(=900)
Suy ra ΔAOH=ΔBOH∆AOH=∆BOH ( g.c.g)
Suy ra OA=OBOA=OB (hai cạnh tương ứng).
b) Xét ΔAOC∆AOC và ΔBOC∆BOC có:
+) OA=OBOA=OB (cmt)
+) ˆAOC=ˆBOCAOC^=BOC^ (gt)
+) OCOC cạnh chung.
Suy ra ΔAOC=ΔBOC∆AOC=∆BOC (c.g.c)
Suy ra: CA=CBCA=CB ( hai cạnh tương ứng)
ˆOAC=ˆOBCOAC^=OBC^ ( hai góc tương ứng).