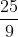Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(-\frac{\pi}{2}< x< 0\Rightarrow sinx< 0\)
\(\Rightarrow sinx=-\sqrt{1-cos^2x}=-\frac{1}{\sqrt{5}}\)

Do x thuộc cung phần tư thứ \(IV\) \(\Rightarrow\left\{{}\begin{matrix}sinx< 0\\cosx>0\end{matrix}\right.\) \(\Rightarrow sinx-cosx< 0\)
\(sinx+cosx=m\Rightarrow\left(sinx+cosx\right)^2=m^2\)
\(\Rightarrow1+2sinx.cosx=m^2\Rightarrow2sinx.cosx=m^2-1\)
Đặt \(P=sinx-cosx< 0\Rightarrow P^2=\left(sinx-cosx\right)^2=1-2sinx.cosx\)
\(\Rightarrow P^2=1-\left(m^2-1\right)=2-m^2\Rightarrow P=-\sqrt{2-m^2}\) (do \(P< 0\))

\(\frac{1-cosx+cos2x}{sin2x-sinx}=\frac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}=\frac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}=\frac{cosx}{sinx}=cotx\)
\(A=sin\left(\frac{\pi}{4}+x\right)-sin\left(\frac{\pi}{2}-\frac{\pi}{4}+x\right)=sin\left(\frac{\pi}{4}+x\right)-sin\left(\frac{\pi}{4}+x\right)=0\)

\(M=sin^2x+cos^2x+2sinx.cosx+cos^2x-sin^2x\)
\(=\left(sinx+cosx\right)^2+\left(cosx-sinx\right)\left(cosx+sinx\right)\)
\(=\left(sinx+cosx\right)\left(sinx+cosx+cosx-sinx\right)\)
\(=2cosx\left(sinx+cosx\right)\)
\(=2\sqrt{2}cosx.cos\left(x-\frac{\pi}{4}\right)\)

Lời giải:
$A=\frac{2\cos \frac{2x+y}{2}\sin \frac{x}{2}}{2\sin \frac{2x+y}{2}.\cos \frac{x}{2}}-\frac{2\cos \frac{2x+y}{2}\cos \frac{x}{2}}{-2\sin \frac{2x+y}{2}\sin \frac{x}{2}}$
$=\tan \frac{x}{2}.\cot \frac{2x+y}{2}+\cot \frac{x}{2}.\cot \frac{2x+y}{2}=\cot \frac{2x+y}{2}(\tan \frac{x}{2}+\cot \frac{x}{2})$

Ta có : sin2 x + cos2 x = 1 ⇒ sin2 x = 1 – cos2 x.
⇒ P = 3.sin2 x + cos2 x
= 3.(1 – cos2x) + cos2 x
= 3 – 3.cos2x + cos2x
= 3 – 2.cos2x
= 3 – 2.(1/3)2
= 3 – 2/9
= 25/9.

Chọn C.
Ta có: sin2x + cos2x = 1 ⇒ sin2x = 1 – cos2x = 1 – 4/9 = 5/9
Vậy: ![]()

\(P=\frac{sin^2x+cos^2x+2sinx.cosx-1}{\sqrt{2}\left(cosx.cos\frac{\pi}{4}-sinx.sin\frac{\pi}{4}\right).cotx}-\frac{1}{cosx-sinx}\)
\(=\frac{2sinx.cosx}{\left(cosx-sinx\right).\frac{cosx}{sinx}}-\frac{1}{cosx-sinx}=\frac{2sin^2x}{cosx-sinx}-\frac{1}{cosx-sinx}\)
\(=\frac{2sin^2x-1}{cosx-sinx}=\frac{2sin^2x-\left(sin^2x+cos^2x\right)}{cosx-sinx}=\frac{sin^2x-cos^2x}{cosx-sinx}\)
\(=\frac{\left(sinx-cosx\right)\left(sinx+cosx\right)}{cosx-sinx}=-\left(sinx+cosx\right)\)

Giả sử các biểu thức đã cho đều xác định
a/ \(\dfrac{1+sin^2x}{1-sin^2x}=\dfrac{1+sin^2x}{cos^2x}=\dfrac{1}{cos^2x}+\dfrac{sin^2x}{cos^2x}+1+tan^2x+tan^2x=1+2tan^2x\)
b/ \(\dfrac{sinx}{1+cosx}+\dfrac{1+cosx}{sinx}=\dfrac{sin^2x+\left(1+cosx\right)^2}{\left(1+cosx\right)sinx}=\dfrac{sin^2x+cos^2x+2cosx+1}{\left(1+cosx\right)sinx}\)
\(=\dfrac{1+2cosx+1}{\left(1+cosx\right)sinx}=\dfrac{2+2cosx}{\left(1+cosx\right)sinx}=\dfrac{2\left(1+cosx\right)}{\left(1+cosx\right)sinx}=\dfrac{2}{sinx}\)
c/ \(\dfrac{1-sinx}{cosx}=\dfrac{\left(1-sinx\right)cosx}{cos^2x}=\dfrac{\left(1-sinx\right)cosx}{1-sin^2x}\)
\(\dfrac{\left(1-sinx\right)cosx}{\left(1-sinx\right)\left(1+sinx\right)}=\dfrac{cosx}{1+sinx}\)
d/ \(\left(1-cosx\right)\left(1+cot^2x\right)=\left(1-cosx\right).\dfrac{1}{sin^2x}\)
\(=\dfrac{1-cosx}{1-cos^2x}=\dfrac{1-cosx}{\left(1-cosx\right)\left(1+cosx\right)}=\dfrac{1}{1+cosx}\)
e/ \(1-\dfrac{sin^2x}{1+cotx}-\dfrac{cos^2x}{1+tanx}=1-\dfrac{sin^3x}{sinx\left(1+\dfrac{cosx}{sinx}\right)}-\dfrac{cos^3x}{cosx\left(1+\dfrac{sinx}{cosx}\right)}\)
\(=1-\left(\dfrac{sin^3x}{sinx+cosx}+\dfrac{cos^3x}{sinx+cosx}\right)=1-\left(\dfrac{sin^3x+cos^3x}{sinx+cosx}\right)\)
\(=1-\left(\dfrac{\left(sinx+cosx\right)\left(sin^2x-sinx.cosx+cos^2x\right)}{sinx+cosx}\right)\)
\(=1-\left(1-sinx.cosx\right)=sinx.cosx\)
f/ Bạn ghi đề sai à?
Ta có sin2x + cos2x = 1 => sin2x = 1 – cos2x
Do đó P = 3sin2x + cos2x = 3(1 – cos2x) + cos2x
=> P = 3 – 2cos2x
Với cosx = => cos2x =
=> cos2x =  => P= 3 –
=> P= 3 –  =
=