Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trên nửa mặt phẳng bờ chứa tia Ox , ta có : \(\widehat{xOz}< \widehat{xOy}\left(70^o< 140^o\right)\)
\(\Rightarrow\)tia Oz nằm giữa tia Ox và tia Oy (1)
\(\Rightarrow\widehat{xOz}+\widehat{zOy}=\widehat{xOy}\)
\(70^o+\widehat{zOy}=140^o\)
\(\widehat{zOy}=140^o-70^o\)
\(\widehat{zOy}=70^o\)
\(\Rightarrow\widehat{xOz}=\widehat{zOy}=70^o\)(2)
Từ (1) và (2) \(\Rightarrow\)Oz là tia phân giác của \(\widehat{xOy}\)
b) Ta có : \(\widehat{xOy}\)và \(\widehat{yOt}\)là 2 góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{yOt}=180^o\)
\(140^o+\widehat{yOt}=180^o\)
\(\widehat{yOt}=180^o-140^o\)
\(\widehat{yOt}=40^o\)
Cậu tự vẽ hình nha:>
a) _ Ta có: \(\widehat{xOz}< \widehat{xOy}\left(70^o< 140^o\right)\)
\(=>\) Oz nằm giữa 2 tia Ox và Oy (1)
_ Lại có :\(\widehat{xOz}+\widehat{zOy}=\widehat{xOy}\)
\(=>\widehat{zOy}=\widehat{xOy}-\widehat{xOz}=140^o-70^o=70^o\)
\(=>\widehat{xOz}=\widehat{zOy}\left(=70^o\right)\)(2)
_ Từ (1) và (2) :
\(=>\) Oz là tia phân giác của \(\widehat{xOy}\)
b) Ta có:\(\widehat{xOy}+\widehat{yOt}=180^o\)( 2 góc kề bù)
\(=>\widehat{yOt}=180^o-140^o=40^o\)
cậu có thể tham khảo bài làm trên đây ạ, chúc cậu học tốt:>

bạn ơi , sao kí hiệu (xOt)^ là sao thế , hok hỉu , hình 6 dễ thui , bạn cố lên nhoa...TYM

a) Vì tia Ot và tia Oy cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox
mà góc xOt <góc xOy (vì 700 <120o
nên tia Ot nằm giữa hai tia Ox và Oy
b) vì tia Oz là tia đối của tia Ox nên góc xOz =180 độ
góc xOy và góc yOz là hai góc kề bù
suy ra góc xOy +góc yOz=180độ
suy ra 120 độ + góc yOz=180độ
góc yOz=80độ
c) góc xOy và góc yOz là hai góc kề bù nên tia Oy nằm giữa hai tia Ox và Oz

Giải: a) Tia Oy nằm giữa Ox và Oz(vì góc xOy < góc xOz) nên góc xOy + góc yOz = xOz
=> góc yOz =góc xOz - góc xOy = 1200 - 400 = 800
b) Ta có: góc xOy + góc xOt = 1800 (kề bù)
=> góc xOt = 1800 - góc xOy = 1800 - 400 = 1400
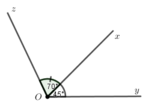
Vì z O x ^ và z O x ^ là hai góc kề bù nên
z O x ^ + x O t ^ = 180 ∘ 70 ∘ + x O t ^ = 180 ∘ x O t ^ = 180 ∘ − 70 ∘ x O t ^ = 110 ∘