Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

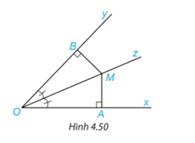
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)

A nằm trên tia phân giác của góc xOy nên A cách đều OB và OC.
=>AB=AC. ABOC là hình vuông mà AB=AC => ABOC là hình vuông.
Trên tia Ox đặt điểm G sao cho BG=CE.
Dê dàng chứng minh tam giác ABG= tam giác ACE(c.g.c)
=> góc BGA = góc AEC
=>góc BAG= góc CAE
Mà góc CAE= góc EAD => 3 góc EAC,DAE,BAG bằng nhau.
Có góc BAD + góc DAE + góc EAC=90 độ; góc EAC + góc AEC = 90 độ
=> góc BAD + góc DAE= góc AEC
Mà góc DAE = góc BAG => góc BAG + góc BAD = góc GAD = góc AEC = góc DGA
=> Tam giác DGA cân tại D => DG=DA
=>DB+BG=DA
=>DA=DB+CE (đpcm)

a, Xét tg AOM và tg MOB
Có : A=B=90
OM cạnh chung
góc AOM= góc MOY (vì OZ là tia fan giác góc xOy)
b.ko bt
 hih đó nhé
hih đó nhé