Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Phân tích
Giả sử đường tròn tâm I dựng được thỏa mãn điều kiện bài toán.
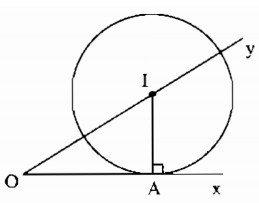
− Đường tròn tâm I tiếp xúc với Ox tại A nên I nằm trên đường thẳng vuông góc với Ox kẻ từ A.
− Tâm I nằm trên tia Oy nên I là giao điểm của Oy và đường thẳng vuông góc với Ox tại A.
* Cách dựng
− Dựng đường vuông góc với Ox tại A cắt Oy tại I.
− Dựng đường tròn (I; IA).
* Chứng minh
Ta có: I thuộc Oy, OA ⊥ IA tại A.
Suy ra Ox là tiếp tuyến của đường tròn ( I;IA)
hay (I; IA) tiếp xúc với Ox.
* Biện luận
Vì góc xOy là góc nhọn nên đường thẳng vuông góc với Ox tại A luôn cắt tia Oy nên tâm I luôn xác định và duy nhất.


* Phân tích
Giả sử đường tròn tâm I dựng được thỏa mãn điều kiện bài toán.
− Đường tròn tâm I tiếp xúc với Ox tại A nên I nằm trên đường thẳng vuông góc với Ox kẻ từ A.
− Tâm I nằm trên tia Oy nên I là giao điểm của Oy và đường thẳng vuông góc với Ox tại A.
* Cách dựng
− Dựng đường vuông góc với Ox tại A cắt Oy tại I.
− Dựng đường tròn (I; IA).
* Chứng minh
Ta có: I thuộc Oy, OA ⊥ IA tại A.
Suy ra Ox là tiếp tuyến của đường tròn ( I;IA)
hay (I; IA) tiếp xúc với Ox.
* Biện luận
Vì góc xOy là góc nhọn nên đường thẳng vuông góc với Ox tại A luôn cắt tia Oy nên tâm I luôn xác định và duy nhất.

* Phân tích
Giả sử đường tròn tâm I dựng được thỏa mãn điều kiện bài toán.
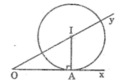
- Đường tròn tâm I tiếp xúc với Ox tại A nên I nằm trên đường thẳng vuông góc với Ox kẻ từ A
- Tâm I nằm trên tia Oy nên I là giao điểm của Oy và đường thẳng vuông góc với Ox tại A
* Cách dựng
- Dựng đường vuông góc với Ox tại A cắt Oy tại I
- Dựng đường tròn (I; IA)
* Chứng minh
Ta có: I thuộc Oy; OA ⊥ IA tại A
Suy ra Ox là tiếp tuyến của đường tròn (I; IA) hay (I; IA) tiếp xúc với Ox.
* Biện luận
Vì góc (xOy) là góc nhọn nên đường thẳng vuông góc với Ox tại A luôn cắt tia Oy nên tâm I luôn xác định và duy nhất.

Tâm O nằm trên đường trung trực của BC và tâm O thuộc tia Ay. Nên tâm O là giao điểm của tia Ay và đường trung trực của BC.

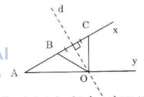
- Tâm O là giao điểm giữa đường trung trực của BC và tia Ay. Nên ta có cách dựng:
+ Dựng đường trung trực (d) của BC. (d) cắt tia Ay tại O.
+ Vẽ đường tròn (O, OB). Đường tròn này đi qua B, C. Đó là đường tròn cần dựng.
- Chứng minh:
+ Vì O ∈ đường trung trực (d) của BC nên OB = OC. Suy ra (O, OB) đi qua B, C
+ Vì O ∈ Ay nên (O, OB) thỏa mãn điều kiện đề bài.

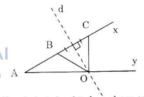
- Tâm O là giao điểm giữa đường trung trực của BC và tia Ay. Nên ta có cách dựng:
+ Dựng đường trung trực (d) của BC. (d) cắt tia Ay tại O.
+ Vẽ đường tròn (O, OB). Đường tròn này đi qua B, C. Đó là đường tròn cần dựng.
- Chứng minh:
+ Vì O ∈ đường trung trực (d) của BC nên OB = OC. Suy ra (O, OB) đi qua B, C
+ Vì O ∈ Ay nên (O, OB) thỏa mãn điều kiện đề bài.

* Cách dựng:
- Dựng đường trung trực của DE cắt Ax tại M
- Dựng đường tròn tâm M bán kính MD
* Chứng minh:
Theo cách dựng ta có: M ∈ Ox
MD = ME (tính chất đường trung trực)
Suy ra: E ∈ (M; MD).