Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựa vào tính chất cộng góc, ta tính được B O M ^ = 90 ° từ đó tính được B O N ^ = 40 ° vậy M O N ^ > B O N ^
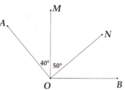

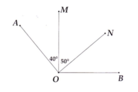
a) Dựa vào tính chất cộng góc, ta tính được B O M ^ = 90 °
từ đó tính được B O N ^ = 40 °
vậy M O N ^ > B O N ^
b) Ta có B O N ^ = 40 ° ; A O N ^ = 90 °
Các cặp góc bằng nhau là:
A O M ^ và B O N ^ ; A O N ^ và B O M ^

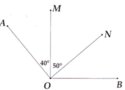
Ta có B O N ^ = 40 ° , A O N ^ = 90 °
Các cặp góc bằng nhau là: A O M ^ v à B O N ^ ; A O N ^ v à B O M ^