Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D

a: f(x) có ĐKXĐ là 6-x>=0
=>x<=6
=>\(A=(-\infty;6]\)
g(x) có ĐKXĐ: là 2x+1<>0
=>\(x< >-\dfrac{1}{2}\)
=>\(B=R\backslash\left\{-\dfrac{1}{2}\right\}\)
\(A\cap B=(-\infty;6]\cap\left(R\backslash\left\{-\dfrac{1}{2}\right\}\right)\)
\(=(-\infty;6]\backslash\left\{\dfrac{1}{2}\right\}\)
\(A\cup B=R\)
\(A\text{B}=(-\infty;6]\backslash\left(R\backslash\left\{-\dfrac{1}{2}\right\}\right)=\left\{-\dfrac{1}{2}\right\}\)
\(B\backslash A=\left(6;+\infty\right)\)

Vẽ đồ thị:
- Vẽ đồ thị hàm số y = f(x) = x + 1 qua hai điểm (0; 1) và (-1; 0).
- Vẽ đồ thị hàm số y = g(x) = 3 - x qua hai điểm (0; 3) và (3; 0)
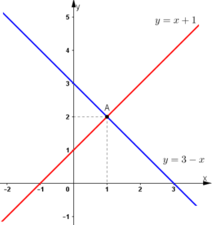
a) Nghiệm của phương trình f(x) = g(x) chính là hoành độ giao điểm của hai đường thẳng y = f(x) và y = g(x).
Giao điểm của hai đường thẳng y = x + 1 và y = 3 – x là điểm A(1; 2).
Do đó phương trình f(x) = g(x) có nghiệm x = 1.
Kiểm tra bằng tính toán:
f(x) = g(x) ⇔ x + 1 = 3 - x ⇔ 2x = 2 ⇔ x = 1.
b) Khi x > 1 thì đồ thị hàm số y = f(x) nằm phía trên đồ thị hàm số y = g(x), hay với x > 1 thì f(x) > g(x).
Kiểm tra bằng tính toán:
f(x) > g(x) ⇔ x + 1 > 3 - x ⇔ 2x > 2 ⇔ x > 1.
c) Khi x < 1 thì đồ thị hàm số y = f(x) nằm phía dưới đồ thị hàm số y = g(x), hay với x < 1 thì f(x) < g(x).
Kiểm tra bằng tính toán:
f(x) < g(x) ⇔ x + 1 < 3 - x ⇔ 2x < 2 ⇔ x < 1.

1:
\(f\left(x\right)=g\left(x\right)\cdot p\left(x\right)\)
=>\(p\left(x\right)=\dfrac{f\left(x\right)}{g\left(x\right)}\)
\(=\dfrac{x^5-3x^4+7x^3-9x^2+8x-2}{x^2-2x+a}\)
Để P(x) tồn tại với mọi x thì \(x^2-2x+a< >0\)(2) với mọi x
Giả sử \(x^2-2x+a=0\)(1)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot a=4-4a\)
Để phương trình (1)có nghiệm thì 4-4a>=0
=>a<=1
Do đó: Để bất phương trình (2) luôn đúng với mọi x thì a>1
Bài 3:
1:
AH=AO
=>H trùng với O
=>Tâm đường tròn ngoại tiếp ΔABC trùng với trực tâm của tam giác
=>ΔABC đều
=>\(\widehat{BAC}=60^0\)

a)F(x)=5x2-7+6x-8x3-x4=\(x^4-8x^3+5x^2+6x-7\)
\(G\left(x\right)=x^4+5+8x^3-5x^2=x^4+8x^3-5x^2+5\)
b)\(F\left(x\right)+G\left(x\right)=x^4-8x^3+5x^2+6x-7+x^4+8x^3-5x^2+5\)
\(=x^4+x^4-8x^3+8x^3+5x^2-5x^2+6x-7+5\)
=\(2x^4+6x-2\)
\(F\left(x\right)-G\left(x\right)=x^4-8x^3+5x^2+6x-7-x^4-8x^3+5x^2-5\)
\(=x^4-x^4-8x^3-8x^3+5x^2+5x^2+6x-7-5\)
=-16x3+10x2+6x-12