Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Khi \(m=0\Rightarrow y=x-1\) nên hàm số không có cực trị
- Khi \(m\ne0\Rightarrow y'=3mx^2+6mx-\left(m-1\right)\)
hàm số không có cực trị khi và chỉ chỉ y' = 0 không có nghiệm hoặc có nghiệm kép
\(\Leftrightarrow\Delta'=9m^2+3m\left(m-1\right)=12m^2-3m\le0\) \(\Leftrightarrow0\le m\)\(\le\frac{1}{4}\)

4 vị trí đều có sự xuất hiện của m, ko còn gì để nói với người ra đề
Do hàm \(f\left(x\right)\) là bậc 3 nên \(y=\left|f\left(x\right)\right|\) có 5 cực trị khi và chỉ khi \(y=f\left(x\right)\) có 2 cực trị nằm về 2 phía trục hoành
\(m\ne2\); ta có \(f'\left(x\right)=g\left(x\right)=3\left(m-2\right)x^2-4\left(2m-3\right)x+\left(5m-3\right)\)
Quy trình giải tiếp theo:
- \(\Delta'>0\)
- Tìm phương trình đường thẳng đi qua 2 cực trị của hàm số bằng cách chia y cho \(y'\) và lấy phần dư, sẽ được một phương trình đường thẳng \(d\) có dạng \(y=ax+b\) trong đó a, b phụ thuộc vào \(m\)
- Tìm giao điểm của d với Ox: \(A\left(-\frac{b}{a};0\right)\)
- Hàm số có 2 cực trị nằm về 2 phía trục hoành khi: \(x_1< -\frac{b}{a}< x_2\) với \(x_1;x_2\) là nghiệm của pt \(f'\left(x\right)=0\)
\(\Leftrightarrow\left(m-2\right).g\left(-\frac{b}{a}\right)< 0\)
Tự luận chắc là chỉ có 1 cách này :(

Hàm số có cực đại, cực tiểu khi m<2. Tọa độ các điểm cực trị là :
\(A\left(0;m^2-5m+5\right);B\left(\sqrt{2-m};1-m\right);C\left(-\sqrt{2-m};1-m\right)\)

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m

đi từ hướng làm để ra được bài toán:
Ta thấy muốn f(|x|) có 5 điểm cực trị thì f'(x) phải có 2 điểm cực trị dương
giải f'(x)=0 \(\left\{{}\begin{matrix}x=1\\x^2-2\left(m+1\right)x+m^2-1=0\left(2\right)\end{matrix}\right.\) phương trình (2) phải có 2 nghiệm phân biệt trái dấu nhau
Ta có: \(\Delta>0\Leftrightarrow m>-1\)
Theo yêu cầu bài toán: \(m^2-1>0\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>1\end{matrix}\right.\)


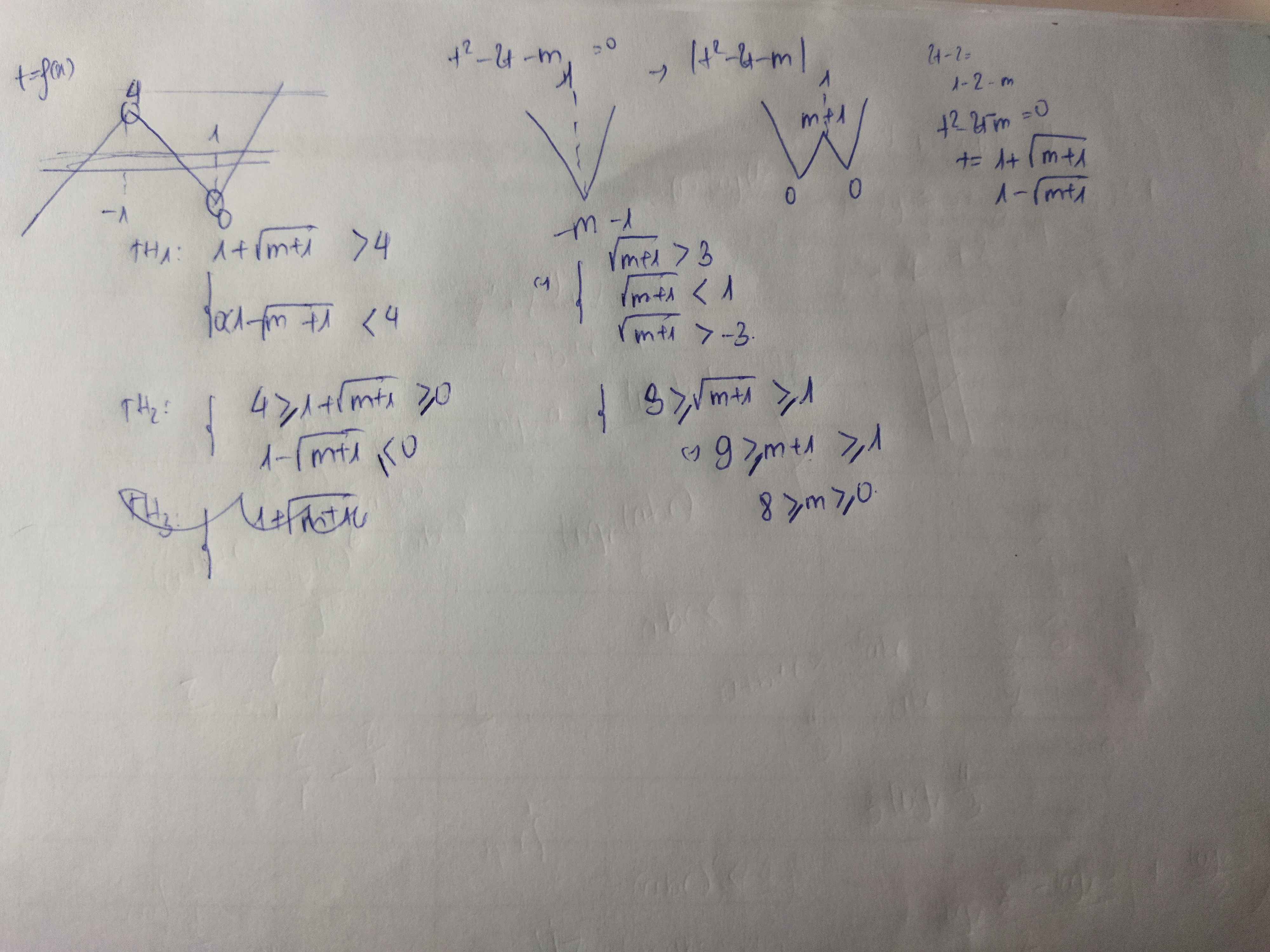 9 đko nhỉ
9 đko nhỉ
Gọi số điểm cực trị dương của \(f\left(x\right)\) là k thì số cực trị của \(f\left(\left|x\right|\right)\) là \(2k+1\)
Do đó để \(g\left(x\right)\) có 5 cực trị thì \(f'\left(x\right)=0\) có 2 nghiệm dương
\(\Rightarrow x^2+2mx+5=0\) có 2 nghiệm dương phân biệt
\(\Rightarrow\left\{{}\begin{matrix}\Delta'=m^2-5>0\\x_1+x_2=-2m>0\\x_1x_2=5>0\end{matrix}\right.\) \(\Rightarrow m< -\sqrt{5}\)
\(\Rightarrow m=\left\{-3;-4;-5;...;-9\right\}\)