Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Học sinh tự làm
b) Chứng minh A N 1 2 N C ⇒ S A M E = S A E N ⇒ E M = E N
hay E là trung điểm MN.
c) Chứng minh được EG//HF và HE/FG nên EHFG là hình bình hành; Mặt khác BM ^ NC (do AB ^ AC)
Suy ra EHFG là hình chữ nhật


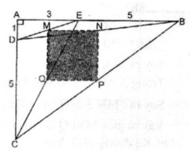
Trong ΔEDC ta có:
M là trung điểm của ED
Q là trung điểm của EC
nên MQ là đường trung bình của ∆ EDC
⇒ MQ = 1/2 CD = 2,5 (cm) và MQ // CD
Trong ∆ BDC ta có:
N là trung điểm của BD
P là trung điểm của BC
nên NP là đường trung bình của ∆ BDC
⇒ NP = 1/2 CD = 2,5 (cm)
Trong ∆ DEB ta có:
M là trung điểm của DE
N là trung điểm của DB
nên MN là đường trung bình của ∆ DEB
⇒ MN = 1/2 BE = 2,5 (cm) và MN // BE
Trong ∆ CEB ta có:
Q là trung điểm của CE
P là trung điểm của CB
nên QP là đường trung bình của ∆ CEB
⇒ QP = 1/2 BE = 2,5 (cm)
Suy ra: MN = NP = PQ = QM (1)
MQ // CD hay MQ // AC
AC ⊥ AB (gt)
⇒ MQ ⊥ AB
MN // BE hay MN // AB
Suy ra: MQ ⊥ MN hay (QMN) = 90 0 (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình vuông
S M N P Q = M N 2 = 2 , 5 2 = 6 , 75 c m 2

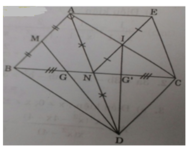
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)