Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình( tự vẽ)
a) Chú ý: \(\widehat{AEB}=\widehat{AFB}=90\)(góc chắn nửa đường tròn) => H là trực tâm tam giác ABC
=> tứ giác AIFC nội tiếp (do \(\widehat{AIC}=\widehat{AFC}=90\)) => góc CIF= góc CAF
mà góc CAF=\(\frac{1}{2}\)góc EOF
mà EF=R => tam giác OEF đều => EOF =60 => CIF=30
b)
tam giác vuông AIC đồng dạng với tam giác vuông AEB (g-g)
=> AE.AC=AI.AB
Tương tự tam giác BIC đồng dạng BFA
=> BF.BC=BI.AB
Vậy: AE.AC+BF.BC=AB(AI+IB)=AB\(^2\)=4R\(^2\)=const (ĐPCM)

a: góc MHO+góc MKO=180 độ
=>MHOK nội tiêp
C,N,D,F cùng thuộc (O)
nên CNDF nội tiếp
b: Xét ΔCKM vuông tại K và ΔCHO vuông tại H có
góc KCM chung
=>ΔCKM đồng dạng voi ΔCHO
=>CK/CH=CM/CO
=>CK*CO=CH*CM

Đây là bài toán con bướm . Cách làm cơ bản là c/m tg IMN cân tại O như sau (mình nêu các bước thôi).
- tgEDI và tgCFI đồng dạng
- Gọi P, Q trung điểm DE và CF suy ra hai tứ giác MPOI; NQOI nội tiếp suy ra ^MOI = ^MPI và ^NOI = ^NQI
- Ch/m hai tg DPI và FQI (cgc) (Chú ý lấy từ tgEDI và tgCFI đồng dạng )nên ^DPI = ^FOI suy ra ^MOI = ^NOI vậy OI đường cao và phân giác nên tg MNO cân suy ra IM = IN

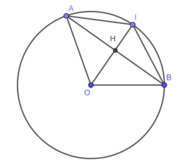
Suy ra : IA =IB (hai cung bằng nhau căng hai dây bằng nhau)
Hay I nằm trên đường trung trực của AB
Mà OA =OB (=R)
Nên O nằm trên đường trung trực của AB
Suy ra OI là đường trung trực của AB
Vì H là trung điểm của AB nên OI đi qua trung điểm H
Vậy ba điểm I, H, O thẳng hàng

Vì I là điểm chính giữa của cung AB nên IA=IB
=>I nằm trên đường trung trực của AB(1)
Ta có: HA=HB
nên H nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,I thẳng hàng