Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) OB=OC (=R) VÀ AB=AC(/c 2 tt cắt nhau)\(\Rightarrow\)OA LÀ ĐƯỜNG TRUNG TRỤC CỦA BC. b) \(BD\perp AB\)(t/c tt) và BE \(\perp AC\)(A \(\varepsilon\left(O\right)\)đường kính BC ). Aps dụng hệ thúc lượng ta có AE*AC=AB\(^2\)=AC\(^2\).
c) c/m OD\(^2=OB^2=OH\cdot OA\)và OH*OA=OK*OF ( \(\Delta OAK\omega\Delta OFH\left(g-g\right)\))\(\Rightarrow\frac{OD}{OF}=\frac{OK}{OD}\)mà góc FOD chung\(\Rightarrow\Delta OKD\omega\Delta ODF\left(c-g-c\right)\Rightarrow\widehat{ODF}=\widehat{OKD}=90\Rightarrow OD\perp DF\Rightarrowđpcm\)

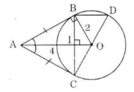
Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)

a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>ΔABC cân tại A
b: Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC tại I và I là trung điểm của BC
c: Xét ΔOBA vuông tại B có \(BO^2+BA^2=OA^2\)
=>\(BA^2+3^2=5^2\)
=>\(BA^2=25-9=16\)
=>\(BA=\sqrt{16}=4\left(cm\right)\)
Xét ΔBOA vuông tại B có BI là đường cao
nên \(BI\cdot OA=BO\cdot BA\)
=>\(BI\cdot5=3\cdot4=12\)
=>BI=12/5=2,4(cm)
d: Ta có: ΔABI vuông tại I
=>\(IB^2+AI^2=AB^2\)
=>\(IB^2=AB^2-AI^2\left(3\right)\)
Ta có: ΔOIC vuông tại I
=>\(OC^2=OI^2+CI^2\)
=>\(CI^2=OC^2-OI^2\left(4\right)\)
I là trung điểm của BC
=>IB=IC(5)
Từ (3),(4),(5) suy ra \(AB^2-AI^2=OC^2-OI^2\)
=>\(AB^2-OC^2=AI^2-OI^2\)
a: Xét tứ giác OBAC có góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc với BC
c: OI*OA=OB^2=OB*OC