Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác vuông $MBO$ vuông tại $B$ có đường cao $BH$:
\(\frac{1}{BH^2}=\frac{1}{MB^2}+\frac{1}{BO^2}=\frac{1}{BO^2-HO^2}\)\(\Rightarrow \frac{1}{MB^2}=\frac{1}{27}-\frac{1}{36}=\frac{1}{108}\Rightarrow MB=6\sqrt{3} (\text{cm})\)
b) Thấy rằng $BC$ là trung trực của $AO$ và $AO$ cũng là trung trực của $BC$ nên $BA=BO=OC=AC$
Mặt khác \(\cos(\widehat{BOH})=\frac{1}{2}\) nên \(\cos (\widehat{BOC})\neq 90^0\)
Do đó $OBAC$ là hình thoi
c) Vì $OA$ là trung trực của $BC$ nên với điểm $M\in OA$ thì $MB=MC$ suy ra \(\triangle MBO=\triangle MCO\Rightarrow \widehat {MBO}=\widehat{MCO}=90^0\Rightarrow MC\perp CO\)
Do đó $MC$ là tiếp tuyến của $(O)$

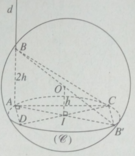
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).

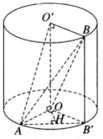
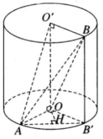
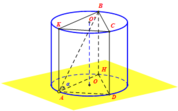
Vì trục OO’ vuông góc với các đáy nên OO′ ⊥ OA; OO′ ⊥ O′B. Vậy các tam giác AOO’ và BO’O vuông tại O và O’.
Theo giả thiết ta có AO ⊥ O′B mà AO ⊥ OO′ ⇒ AO ⊥ (OO′B). Do đó, AO ⊥ OB nên tam giác AOB vuông tại O. Tương tự, ta chứng minh được tam giác AO’B vuông tại O’. Thể tích hình chóp OABO’ là:
![]()
Hay
![]()

Câu này còn 1 ý nữa, nên ý trên em không ra, em không biết giải ý dưới thế nào ạ!
b) Một mặt phẳng vuông góc với đường thẳng e cắt d, delta, e lần lượt ở A1, M1, B1. Chứng minh rằng tam giác A1M1B1 là vuông.

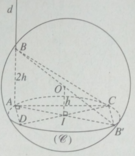
Diện tích tam giác BCD bằng:
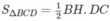
Diện tích này lớn nhất khi AI // CD.

- Nếu H nằm ở nửa dưới đoạn SO thì \(R\ge\dfrac{SO}{2}=\dfrac{3}{2}\)
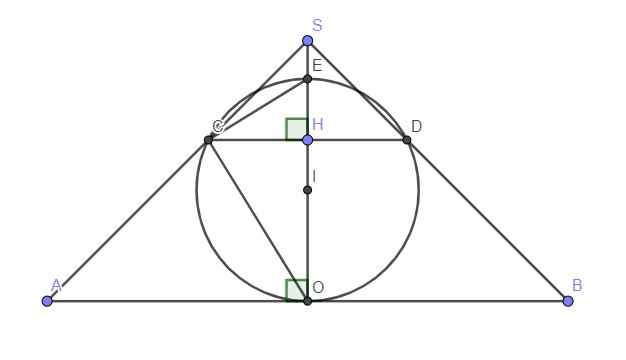
- Nếu H nằm ở nửa trên đoạn SO, thực hiện mặt cắt qua trục nón như hình vẽ
\(SO=OA=3\Rightarrow SOA\) vuông cân \(\Rightarrow SCH\) vuông cân
\(\Rightarrow CH=SH=3-OH=3-\left(R+IH\right)=3-R-\sqrt{R^2-CH^2}\)
\(\Rightarrow3-R=CH+\sqrt{R^2-CH^2}\le\sqrt{2\left(CH^2+R^2-CH^2\right)}=R\sqrt{2}\)
\(\Rightarrow R\left(\sqrt{2}+1\right)\ge3\Rightarrow R\ge\dfrac{3}{\sqrt{2}+1}=3\left(\sqrt{2}-1\right)\)
\(V_{min}=\dfrac{4}{3}\pi R_{min}^3=8,037\)

Đường tròn tâm O có bán kính bằng r 2 2 tiếp xúc với AB’ tại H là trung điểm của AB’. Do đó mặt phẳng ( α ) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên ( α ) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng r 2 2
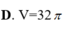
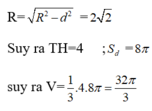

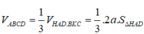

a: Ta có: ΔOMN cân tại O
mà OH là đường cao
nên H là trung điểm của MN
Xét tứ giác BMCN có
H là trung điểm chung của MN và BC
BC vuông góc với MN
DO đó: BMCN là hình thoi
b: Xét (O') có
ΔAGC nội tiếp
AC là đường kính
Do đó: ΔAGC vuông tại G
=>CG vuông góc với AM
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>MB vuông góc với AM
=>MB//CG
CMBN là hình thoi nên CN//MB
=>CN vuông góc với AM
=>C,N,G thẳng hàng