Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO⊥AB
mà ΔOAB cân tại O
nên K là trung điểm của AB

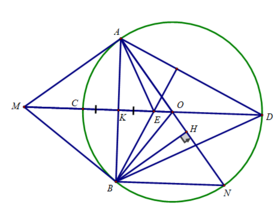
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB

a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b; Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB

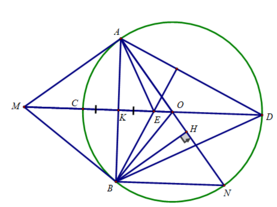
a) Ta có:
MA = MB ( tính chất 2 tiếp tuyến cắt nhau)
OA = OB ( cùng bằng bán kính đường tròn (O)
⇒ OM là đường trung trực của AB
OM ∩ AB = K ⇒ K là trung điểm của AB

Do MA là tiếp tuyến \(\Rightarrow OA\perp MA\) hay tam giác OAM vuông tại A
Áp dụng định lý Pitago:
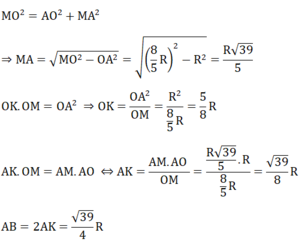
\(MA=\sqrt{OM^2-OA^2}=\sqrt{\left(\dfrac{8R}{5}\right)^2-R^2}=\dfrac{R\sqrt{39}}{5}\)
Theo t/c hai tiếp tuyến cắt nhau ta có \(AM=BM\)
Mà \(OA=OB=R\Rightarrow OM\) là trung trực AB \(\Leftrightarrow\left\{{}\begin{matrix}OM\perp AB\\AK=BK\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông OAM:
\(AK.OM=OA.AM\Rightarrow AK=\dfrac{OA.AM}{OM}=\dfrac{R\sqrt{39}}{8}\)
\(\Rightarrow AB=2AK=\dfrac{R\sqrt{39}}{4}\)
Áp dụng định lý Pitago trong tam giác vuông AOK:
\(OK=\sqrt{OA^2-AK^2}=\sqrt{R^2-\left(\dfrac{R\sqrt{39}}{8}\right)^2}=\dfrac{5R}{8}\)
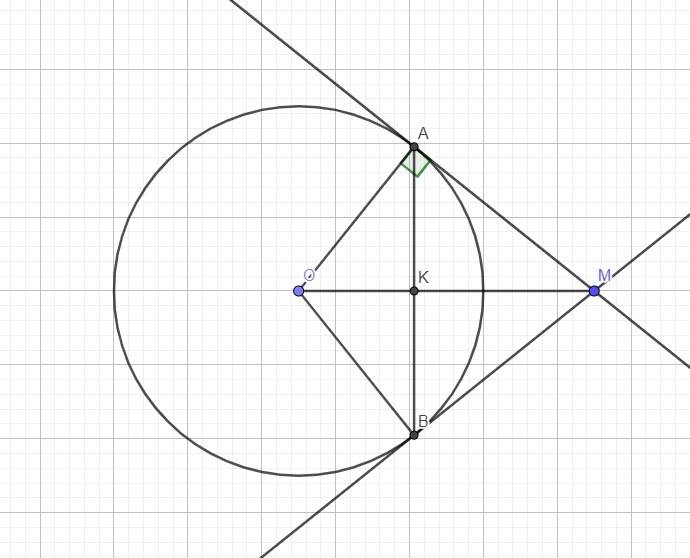

O A B M H C D K F I
a/
Xét tg vuông AMO và tg vuông BMO có
MA=MB (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn)
OA=OB=R
=> tg AMO = tg BMO (2 tg vuông có 2 cạnh góc vuông bằng nhau)
\(\Rightarrow\widehat{AMO}=\widehat{BMO}\)
Xét tg MAB có
MA=MB (cmt) => tg MAB cân tại M
\(\widehat{AMO}=\widehat{BMO}\) (cmt)
\(\Rightarrow OM\perp AB\) (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao)
Xét tg vuông AMO có
\(AM^2=MO.MH\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giưa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
b/
Ta có \(\widehat{ADC}=90^o\) (góc nt chắn nửa đường tròn) => tg ACD vuông tại D \(\Rightarrow AD\perp MC\)
Xét tg vuông AMC có
\(AM^2=MD.MC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giưa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
Ta có
\(AM^2=MO.MH\) (cmt)
\(\Rightarrow MH.MO=MD.MC\)
c/ Xét tg AMK có
\(OM\perp AB\left(cmt\right)\Rightarrow OH\perp AK\)
\(AD\perp MC\left(cmt\right)\Rightarrow AD\perp MK\)
\(\Rightarrow KI\perp AB\) (trong tg 3 đường cao đồng quy)
Phần còn lại không biết điểm E là điểm nào?

a.
Ta có \(MA=MB\) (t/c hai tiếp tuyến cắt nhau)
\(OA=OB=R\)
\(\Rightarrow OM\) là trung trực AB hay OM vuông góc AB
AC là đường kính và B là điểm thuộc đường tròn \(\Rightarrow\widehat{ABC}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ABC}=90^0\Rightarrow AB\perp BC\)
\(\Rightarrow BC||OM\) (cùng vuông góc AB)
b.
Do MA là tiếp tuyến \(\Rightarrow AM\perp AC\) hay tam giác MAC vuông tại A
AC là đường kính và K thuộc đường tròn \(\Rightarrow\widehat{AKC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{AKC}=90^0\) hay AK là đường cao trong tam giác vuông MAC
Áp dụng hệ thức lượng:
\(AC^2=CK.CM\Rightarrow CK.CM=\left(2R\right)^2=4R^2\)
c.
Em có nhầm đề ko nhỉ, vì 2 góc này hiển nhiên bằng nhau, ko cần chứng minh, do 1 góc là góc nội tiếp và 1 góc là góc tạo bởi tiếp tuyến và dây cung, cùng chắn cung BK.
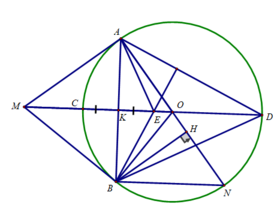
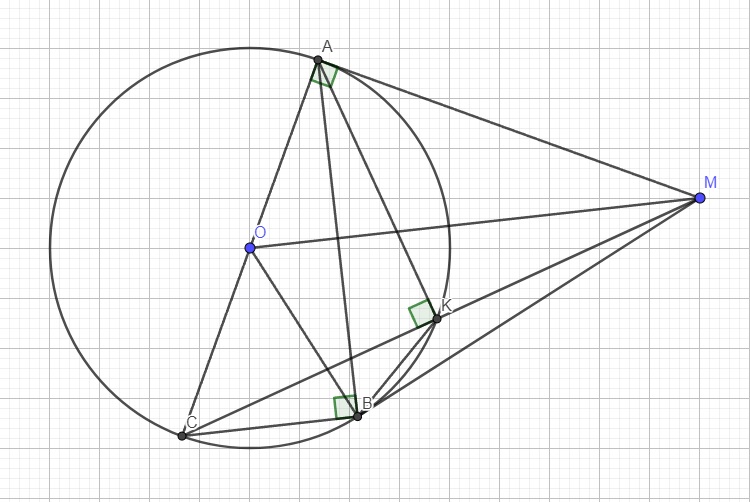
\(a,\)Ta có: \(\hept{\begin{cases}MA=MB\\OA=OB=R\end{cases}}\)
\(\Rightarrow MO\)là đường trung trực của \(AB\)
\(\Rightarrow MO\perp AB\)tại trung điểm \(K\)của \(AB\)
\(b,\)Áp dụng hệ thức lượng vào tam giác vuông \(MAO\)có:
\(+\)\(^{^{ }OA^2+AM^2=OM^2\Leftrightarrow AM=\sqrt{OM^2-OA^2}\Leftrightarrow AM=\sqrt{\frac{8}{5}R)^2-R^2}\Leftrightarrow AM=\frac{\sqrt{39}R}{5}}\)
\(+\) \(AK.OM=OA.AM\Leftrightarrow AK.\frac{8}{5}R\)\(=R.\frac{\sqrt{39}}{5}R\Rightarrow AB=2AK=R\frac{\sqrt{39}}{4}\)
\(+\) \(OA^2=OK.ON\Leftrightarrow OK=\frac{OA^2}{ON}=\frac{R^2}{\frac{8R}{5}}\)\(=\frac{5R}{8}\)
\(c,\)Ta có: \(\widehat{ABN}=90\)(B thuộc đường tròn đường kính AN) \(\Rightarrow BN//MO\left(\perp AB\right)\)
Do đó; \(\hept{\begin{cases}\widehat{AOM=\widehat{ANB}}\\\widehat{AOM=\widehat{BOM}}\end{cases}}\)
\(\Rightarrow\widehat{BOM=\widehat{ANB}}\)
Xét tam giác BHA và MBO có:
\(\hept{\begin{cases}\widehat{BHN}=\widehat{MBO}=90\\\widehat{BNH}=\widehat{BOM}\end{cases}}\)\(\Rightarrow\Delta BHN\simeq\Delta MBO\)\(\Rightarrow\hept{\begin{cases}BH=BN\\MB=MO\end{cases}}\)\(\Rightarrow BH.MO=BN.MB\left(đpcm\right)\)