Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

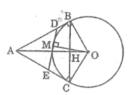
Áp dụng định lí Pitago vào tam giác vuông ABO, ta có:
A O 2 = A B 2 + B O 2
Suy ra: A B 2 = A O 2 - B O 2 = 5 2 - 3 2 = 16
AB = 4 (cm)
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DB + AE + EC
= AB + AC = 2AB = 2.4 = 8 (cm)

a) C/m tg ABCO nội tiếp:
+) Ta có: góc ACO = 90•( vì AC là tiếp tuyến đg tròn (O))
góc ABO = 90•( vì AB là tiếp tuyến đg tròn (O))
+) Xét tg ABOC có: góc ACO+ góc ABO=90•+90•=180•
Mà 2 góc ở vị trí đối nhau
=> tg ABOC nội tiếp đg tròn(dhnb)
b) C/m: CD// AO:
+) Vì AB và AC là 2 tiếp tuyến cắt nhau tại A(gt) => AO là đg pg của góc COB( t/c 2 tiếp tuyến cắt nhau)
=> AO là pg của tam giác COB
Mà tam giác COB cân tại O( OB=OC=R)
=> OA là đg cao của tam giác COB( t/c tam giác cân)
=> OA vuông góc vs CB( t/c) (1)
+) Xét (O) ta có:
BD là đg kính( gt)
góc BCD là góc nội tiếp chắn cung BD
=> góc BCD= 90• ( t/c góc nội tiếp chắn nửa đg tròn)
=> CD vuông góc vs CB(t/c) (2)
Từ(1) và (2) suy ra: CD// OA( từ vuông góc đến song song).
mk chưa ra câu c nên xin lỗi bn nhiều nhé....
a: Gọi H là giao điểm của AO và BC
Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có \(OA^2=OB^2+BA^2\)
=>\(BA^2+3^2=5^2\)
=>\(BA^2+9=25\)
=>\(BA^2=25-9=16\)
=>BA=4(cm)
AB=AC
mà AB=4cm
nên AC=4cm
Xét ΔBAO vuông tại B có BH là đường cao
nên \(BH\cdot OA=OB\cdot BA\)
=>\(BH\cdot5=3\cdot4=12\)
=>BH=12/5=2,4(cm)
H là trung điểm của BC
=>BC=2*BH=2*2,4=4,8(cm)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=4+4+4,8=12,8\left(cm\right)\)
b: Xét (O) có
NM,NB là tiếp tuyến
Do đó: NM=NB và ON là phân giác của góc MOB
ON là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{NOM}\)
Xét (O) có
QM,QC là tiếp tuyến
Do đó: QM=QC và OQ là phân giác của \(\widehat{MOC}\)
OQ là phân giác của góc MOC
=>\(\widehat{MOC}=2\cdot\widehat{MOQ}\)
Chu vi tam giác AQN là:
\(C_{ANQ}=AN+NQ+AQ\)
\(=AN+NM+MQ+AQ\)
\(=AN+NB+QC+AQ\)
=AB+AC
=4+4
=8(cm)
c: Xét ΔBOA vuông tại B có \(sinBOA=\dfrac{BA}{OA}=\dfrac{4}{5}\)
nên \(\widehat{BOA}\simeq53^0\)
Xét (O) có
AB,AC là tiếp tuyến
Do đó: OA là phân giác của góc BOC
=>\(\widehat{BOC}=2\cdot\widehat{BOA}\simeq106^0\)
Ta có: \(\widehat{BOM}+\widehat{COM}=\widehat{BOC}\)
=>\(2\cdot\left(\widehat{NOM}+\widehat{QOM}\right)=\widehat{BOC}\)
=>\(2\cdot\widehat{NOQ}=\widehat{BOC}\)
=>\(\widehat{NOQ}=\dfrac{1}{2}\cdot\widehat{BOC}=\widehat{BOA}\simeq53^0\)