Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A' là giao điểm của đường tròn ngoại tiếp tam giác AEF và tia AB
Ta chứng minh được E,A,N và M, A, F thẳng hàng
=> A đối xứng với A' qua C => B đối xứng với A' qua điểm A mà A' cố định
=> Tâm I của đường tròn ngoại tiếp tam giác BMN nằm trên đường trung trực của đoạn thẳng BA'.

a: ΔODE cân tại O
mà OM là trung tuyến
nên OM vuông góc DE
=>góc OMA=90 độ=góc OCA=góc OBA
=>O,A,B,M,C cùng thuộc 1 đường tròn
b: Xét ΔBSC và ΔCSD có
góc SBC=góc SCD
góc S chung
=>ΔBSC đồng dạng với ΔCSD
=>SB/CS=SC/SD
=>CS^2=SB*SD
góc DAS=gócEBD
=>góc DAS=góc ABD
=>ΔSAD đồng dạng với ΔSBA
=>SA/SB=SD/SA
=>SA^2=SB*SD=SC^2
=>SA=SC
c; BE//AC
=>EH/SA=BH/SC=HJ/JS
mà SA=SC
nênHB=EH
=>H,O,C thẳng hàng

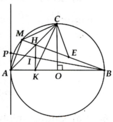
O A B C M K H E d P F I
1) Dễ thấy \(\widehat{HCB}=\widehat{ACB}=90^o\)
tứ giác CBKH có \(\widehat{HKB}=\widehat{HCB}=90^o\)nên là tứ giác nội tiếp
\(\Rightarrow\widehat{HCK}=\widehat{HBK}\)( 1 )
Mà \(\widehat{ACM}=\widehat{ABM}=\frac{1}{2}sđ\widebat{AM}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{ACM}=\widehat{ACK}\)
2) Xét \(\Delta AMC\)và \(\Delta BEC\)có :
AM = BE ; AC = BC ; \(\widehat{MAC}=\widehat{CBE}=\frac{1}{2}sđ\widebat{MC}\)
\(\Rightarrow\Delta AMC=\Delta BEC\)( c.g.c )
\(\Rightarrow MC=EC\)
Ta có : \(\widehat{CMB}=\frac{1}{2}sđ\widebat{BC}=45^o\)
Suy ra \(\Delta ECM\)vuông cân tại C
3) Ta có : \(\frac{AP.MB}{AM}=R=OB\Rightarrow\frac{AP}{MA}=\frac{OB}{MB}\)
Xét \(\Delta APM\)và \(\Delta OBM\), ta có :
\(\frac{AP}{MA}=\frac{OB}{MB}\); \(\widehat{PAM}=\widehat{MBO}=\frac{1}{2}sđ\widebat{AM}\)
\(\Rightarrow\Delta APM\approx\Delta BOM\left(c.g.c\right)\)
\(\Rightarrow\Delta APM\)cân tại P ( vì \(\Delta BOM\)cân tại O )
\(\Rightarrow PA=PM\)
Gọi giao điểm của BM và ( d ) là F ; giao điểm của BP với HK là I
Xét tam giác vuông AMF có PA = PM nên PA = PM = PF
Theo định lí Ta-let, ta có :
\(\frac{HI}{FP}=\frac{BI}{BP}=\frac{KI}{AP}\Rightarrow HI=KI\)
vì vậy PB đi qua trung điểm của HK

a, Chứng minh được H C B ^ = H K B ^ = 90 0
b, A C K ^ = H B K ^ (CBKH nội tiếp)
Lại có: A C M ^ = H B K ^ = 1 2 s đ A M ⏜
=> A C M ^ = A C K ^
c, Chứng minh được:
DMCA = DECB (c.g.c) => MC = CE
Ta có: C M B ^ = C A B ^ = 1 2 s đ C B ⏜ = 45 0
=> DMCE vuông cân tại C
d, Gọi P B ∩ H K = I
Chứng minh được DHKB đồng dạng với DAMB (g.g)
=> H K K B = M A M B = A P R => H K = A P . B K R
Mặt khác: ∆BIK:∆BPA(g.g) => (ĐPCM)