Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B x y C D M O
a/
Xét tg vuông OAC và tg vuông OMC có
OA=OM=R
OC chung
=> tg OAC = tg OMC (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{AOC}=\widehat{MOC}=\dfrac{\widehat{AOM}}{2}\)
Tương tự ta cũng có
tg OBD = tg OMD \(\Rightarrow\widehat{BOD}=\widehat{MOD}=\dfrac{\widehat{BOM}}{2}\)
\(\Rightarrow\widehat{MOC}+\widehat{MOD}=\widehat{COD}=\dfrac{\widehat{AOM}}{2}+\dfrac{\widehat{BOM}}{2}=\dfrac{180^o}{2}=90^o\)
b/
AB+BD nhỏ nhất khi \(M\equiv B\)

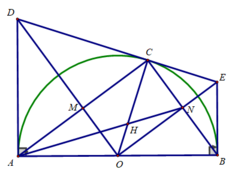
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật
Ta có ABMN là hinh thang vuông với 2 đáy lần luợt là AM, BN
Khi đó dh of tu giac = ABx[AM+BN]/2
Diện tích nhỏ nhất của tứ giác là 2R2 (=ABx[AM+BN]/2=ABxOC), khi tiếp tuyến qua C vg góc 2 tiếp tuyến kia. Và ABMN là HCN.