Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC

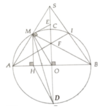
D C O B A F H E S
- SA,SB là tiếp tuyến tại AB => \(SO⊥AB\)tại E => E là trung điểm của AB. H là trung điểm của CD => \(OH⊥CD\)Nên ta có \(\hept{\begin{cases}\widehat{SEF}=90^0\\\widehat{SHF}=90^0\end{cases}}\Rightarrow SEHF\)là tứ giác nội tiếp đường tròn đường kính SF
- Vì SA là tiếp tuyến của (O) tại A =>\(\Delta SAO\)vuông tại A. \(AB⊥SO\Rightarrow\)AE là đường cao nên theo hệ thức lượng trong tam giác vuông ta có:\(OE.OS=OA^2=R^2\) (R không đổi) nên tích OE.OS không phục thuộc vào vị trí của S
- \(HD=\frac{DC}{2}=\sqrt{OD^2-OH^2}=\sqrt{R^2-OH^2}=\sqrt{10^2-6^2}=8\Rightarrow DC=16\)=> SC=SD+CD=4+16=20 Vậy nên \(SA^2=SD.SC\Rightarrow SA=\sqrt{SD.SC}=\sqrt{4.20}=4\sqrt{5}\)
- Ta có O,H cố định nên OH cố định mà AB cắt OH tại F , F thuộc OH nên F là điểm cố định mà AB luôn đi qua khi S chạy trên tia đối của DC

a: Sửa đề: \(EM\cdot AM=MF\cdot OA\)
\(\widehat{EMO}=\widehat{EMF}+\widehat{OMF}\)
=>\(\widehat{EMF}+\widehat{OMF}=90^0\)(1)
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMO}+\widehat{FMO}=\widehat{AMF}=90^0\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{EMF}=\widehat{AMO}\)
=>\(\widehat{EMF}=\widehat{OAM}\)
ΔMEO vuông tại M
=>\(\widehat{MEO}+\widehat{MOE}=90^0\)
=>\(\widehat{MEF}+\widehat{MOE}=90^0\)(3)
Ta có: OM nằm giữa OA và OE
=>\(\widehat{AOM}+\widehat{MOE}=90^0\)(4)
từ (3) và (4) suy ra \(\widehat{MEF}=\widehat{AOM}\)
Xét ΔMEF và ΔAOM có
\(\widehat{MEF}=\widehat{AOM}\)
\(\widehat{EMF}=\widehat{OAM}\)
Do đó: ΔMEF đồng dạng với ΔAOM
=>ME/AO=MF/AM
=>\(ME\cdot AM=AO\cdot MF\)
b: Xét (O) có
ΔAIB nội tiếp
AB là đường kính
Do đó: ΔAIB vuông tại I
=>AI\(\perp\)SB
Xét ΔSAB có
BM,SO là đường cao
BM cắt SO tại F
Do đó; F là trực tâm
=>AF\(\perp\)SB
mà AI\(\perp\)SB(cmt)
và AF,AI có điểm chung là A
nên A,I,F thẳng hàng
