Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 a) Ta có:
a) Ta có:
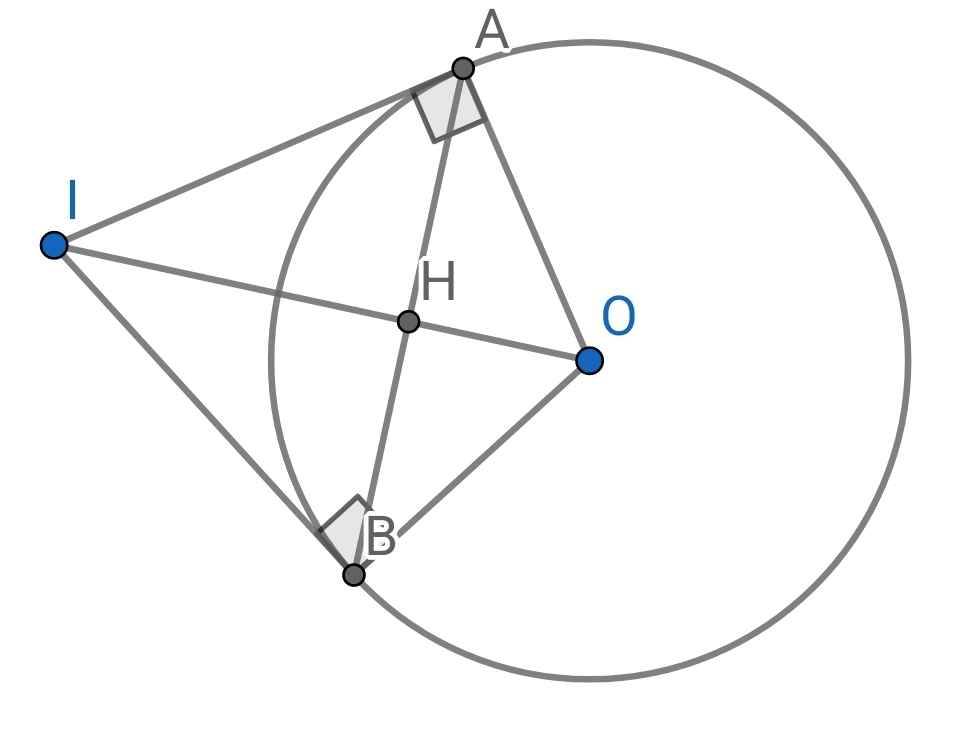
IA = IB (tính chất hai tiếp tuyến cắt nhau)
⇒ I nằm trên đường trung trực của AB (1)
OA = OB (bán kính)
⇒ O nằm trên đường trung trực của AB (2)
Từ (1) và (2) ⇒ OI là đường trung trực của AB
Mà H là giao điểm của AB và OI
⇒ H là trung điểm của AB
⇒ AH = AB : 2 = 24 : 2 = 12 (cm)
Do OI là đường trung trực của AB (cmt)
⇒ AH ⊥ OI
⇒ AH ⊥ HI
∆AHI vuông tại H
⇒ AI² = AH² + IH² (Pytago)
⇒ IH² = AI² - AH²
= 20² - 12²
= 256
⇒ IH = 16 (cm)
∆OAI vuông tại A có AH là đường cao
⇒ AH² = IH.OH
⇒ OH = AH² : IH
= 12² : 16
= 9 (cm)
b) Bán kính của (O) là đoạn OA
Ta có:
OI = OH + IH = 9 + 16 = 25 (cm)
∆OAI vuông tại A
⇒ OI² = IA² + OA² (Pytago)
OA² = OI² - IA²
= 25² - 20²
= 225
⇒ OA = 15 (cm)
Vậy bán kính OA = 15 cm
Để giải bài toán này, chúng ta có thể sử dụng các định lý về tiếp tuyến và đường tròn. Dưới đây là cách giải từng phần của bài toán:
a) Để tính độ dài AH, IH và OH, chúng ta cần sử dụng định lý về tiếp tuyến và đường tròn.
Theo định lý tiếp tuyến, ta có:
AH^2 = AI * AB
AH^2 = 20cm * 24cm
AH^2 = 480cm^2
AH = √480cm ≈ 21.91cm
Theo định lý tiếp tuyến, ta cũng có:
IH^2 = IB * AB
IH^2 = 20cm * 24cm
IH^2 = 480cm^2
IH = √480cm ≈ 21.91cm
Để tính OH, chúng ta cần sử dụng định lý về trung điểm. Vì O là trung điểm của đoạn thẳng IH, nên ta có:
OH = 1/2 * IH
OH = 1/2 * 21.91cm
OH ≈ 10.96cm
Vậy, độ dài AH là khoảng 21.91cm, độ dài IH là khoảng 21.91cm và độ dài OH là khoảng 10.96cm.
b) Để tính bán kính (o), chúng ta có thể sử dụng định lý về đường tròn ngoại tiếp.
Theo định lý đường tròn ngoại tiếp, ta có:
R = AI = 20cm
Vậy, bán kính (o) là 20cm.

a. Ta có: \(\Lambda\)ABO=90 ( do AB là tiếp tuyến của (O))
\(\Lambda\)ACO=90 ( do AC là tiếp tuyến của (O))
\(\Rightarrow\) \(\Lambda\)ABO + \(\Lambda\)ACO = 90 + 90 = 180.
Suy ra: tứ giác ABOC nội tiếp.
b. Ta có: AB,AC lần lượt là tiếp tuyến của (O) nên AB=AC.
\(\Rightarrow\)\(\Delta\)ABC cân tại A lại có AH là tia phân giác nên AH cũng là đường cao
\(\Rightarrow\)AO\(\perp\)BC tại H.
Áp dụng đinh lý Py-ta-go vào \(\Delta\)ABO ta có:
AO2 = AB2 + BO2 = 42 + 32 = 25
\(\Rightarrow\)AO = 5 (cm).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ABO ta được:
AB2 = AH.AO \(\Rightarrow\) AH = \(\dfrac{AB^2}{AO}\)=\(\dfrac{16}{5}\)(cm)
c. Ta có: \(\Lambda\)ACE=\(\Lambda\)ADC ( tính chất của góc tạo bởi tia tiếp tuyến và dây cung )
Xét \(\Delta\)ACE và \(\Delta\)ADC có:
\(\Lambda ACE=\Lambda ADC\)
\(\Lambda\)CAD chung
Do đó: \(\Delta ACE\sim\Delta ADC\) \(\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AC}\) \(\Rightarrow\)AC2 = AD.AE (1)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ACO có:
AC2 = AH.AO (2)
Từ (1) và (2) ,suy ra: AD.AE = AH.AO.
a)Ta có:\(\widehat{ABO};\widehat{ACO}\) lần lượt là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ABO=}\widehat{ACO}=90^{ }\)
\(\Rightarrow\widehat{ABO}+\widehat{ACO}=90+90=180\)
Mà hai góc này đối nhau nên tứ giác ABOC nội tiếb)
b)Theo a) ta có:\(\widehat{ABO}=90\)⇒▲ABO là tam giác vuông tại B đường cao AH.
Áp dụng định lí pytago vào tam giác vuông ABO đường cao AH ta có:
\(AO^2=AB^2+BO^2=4^2+3^2=25\)
\(\Rightarrow\sqrt{AO}=5\) cm.
Áp dụng hệ thức lượng giữa cạnh và đường cao trong ▲vuông ABO ta có:
\(AB^2=AH\cdot AO\)
\(\Rightarrow AH=\dfrac{AB^2^{ }}{AO}=\dfrac{4^2^{ }}{5}=\dfrac{16}{5}\)
I A B O H
a/
+)Vì IA và IB là 2 tt của (O)
=> IA = IB; mặt khác OA = OB
=> IO là trung trực của AB
=> AH = BH = 1/2 AB = 24/2 = 12 (cm)
+) A/dụng định lý pytago vào ΔIAH vuông tại H có: \(IA^2=AH^2+IH^2\)
hay \(20^2=12^2+IH^2\Rightarrow IH^2=256\Rightarrow IH=16\left(cm\right)\)
+) A/dụng hệ thức lượng trong ΔIAO vuông tại A có: \(AH^2=IH\cdot OH\Rightarrow OH=\dfrac{AH^2}{IH}=\dfrac{12^2}{16}=9\left(cm\right)\)
b/ A/dụng hệ thức lượng trong ΔIAO vuông tại A có: \(OA^2=IO\cdot OH=\left(IH+OH\right)\cdot OH=\left(16+9\right)\cdot9=225\)
\(\Rightarrow OA=15\left(cm\right)\) hay R = 15 (cm)