Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

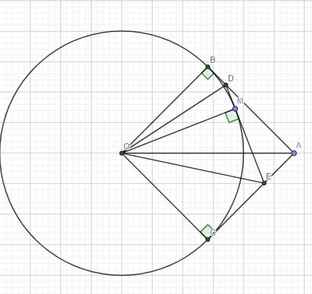
Do AB là tiếp tuyến \(\Rightarrow\Delta OAB\) vuông tại A
Theo định lý Pitago:
\(AB=\sqrt{OA^2-OB^2}=\sqrt{2R^2-R^2}=R\)
\(\Rightarrow AB=OB\Rightarrow\Delta OAB\) vuông cân tại B
Hoàn toàn tương tự ta có tam giác \(OAC\) vuông cân tại C
\(\Rightarrow OBAC\) là hình vuông
b.
Do DB và DM là 2 tiếp tuyến \(\Rightarrow DB=DM\)
Tương tự ta có \(EM=EC\)
\(\Rightarrow\) Chu vi tứ giác ADE:
\(AD+DE+EA=AD+DM+ME+EA=AD+DB+EC+EA=AB+AC=2R\)

a) tứ giác ABOC là hình vuông
vì BAC = 90 (giả thiết)
ABO = 90 (AB là tiếp tuyến)
ACO = 90 (AC là tiếp tuyến)
AB = AC (tính chất 2 tiếp tuyến cắt nhau)

Cho sửa câu c) thành tính góc DOE (:
O B D A M E C
a) Ta có :
\(AB\perp AC=>\widehat{BAC}=90^o\)
\(AB\perp BO=>\widehat{ABO}=90^o\)
\(AC\perp CO=>\widehat{ACO}=90^o\)
Tứ giác ABOC có 3 góc vuông nên nó là hình chữ nhật
Mặt khác : AB = AC (tính chất hai tiếp tuyến cắt nhau)
Suy ra tứ giác ABOC là hình vuông
b. Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2 . 2 = 4 (cm)
c. Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OD là tia phân giác của góc BOM
\(\Rightarrow\widehat{BOD}=\widehat{DOM}=\frac{1}{2}\widehat{BOM}\)
OE là tia phân giác của góc COM
\(\Rightarrow\widehat{COE}=\widehat{EOM}=\frac{1}{2}\widehat{COM}\)
\(\Rightarrow\widehat{DOE}=\widehat{DOM}+\widehat{EOM}=\frac{1}{2}\left(\widehat{BOM}+\widehat{COM}\right)\)
\(=\frac{1}{2}\widehat{COB}=\frac{1}{2}.90^o=45^o\)

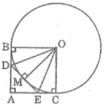
Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)