Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D O
Ta có : \(\begin{cases}AC\perp BD\\BC=CD\end{cases}\)=> AC là đường trung trực của BD
\(\Rightarrow AB=AD\) mà AB không đổi (gt) => AD không đổi mà A cố định
=> D di chuyển trên đường tròn tâm A , bán kính AD


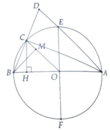
a, Gọi EF là đường kính O ; A B 2 sao cho EF ⊥ AB
Xét trường hợp C chạy trên nửa đường tròn EBF
Chứng minh: ∆OMB = ∆OHC (c.g.c)
=> O M B ^ = O H C ^ = 90 0
Vậy M chạy trên đường tròn đường kính OB
Chứng minh tương tự khi C chạy trên nửa đường tròn EAF, ta được M chạy trên đường tròn đường kính OA
b, Chứng minh ∆ADB cân tại A => AD=AB nên D chạy trên (A;AB)

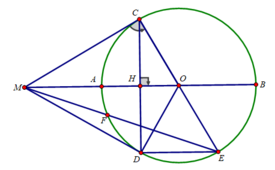
d) Ta có: ∠(CFE) = 90 0 (F thuộc đường tròn đường kính CE)
Lại có CF là đường cao nên MC 2 = MF.ME
Tương tự, ta có: MC 2 = MH.MO
⇒ ME.MF = MH.MO
⇒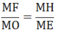
Xét ΔMOF và ΔMEN có:
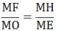
∠(FMO) chung
⇒ ΔMOF ∼ ΔMEN (c.g.c)
⇒ ∠(MOF) = ∠(MEH)


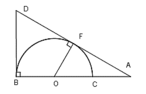
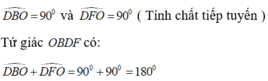
Do C là trung điểm của BD => \(AC\perp BD\) ( AC trùng với đường kính đường tròn ( O ; R ) đi qua C )
\(\Delta ABD\) có AC vừa là đường cao vừa là đường trung tuyến => \(\Delta ABD\) cân tại A
=> AB = AD (không đổi) hay với C di động trên đường tròn ( O ; R ) thì AD không đổi => D di động trên đường tròn ( A ; 2R )