Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

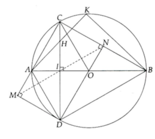
a, HS tự làm
b, Ta có DAHI đồng dạng với DABK (g.g)
=>AH.AK = AI.AB = R 2
c, Chứng minh được I là trung điểm của CD
Từ MCND là hình chữ nhật suy ra MN và CD cắt nhau tại trung điểm của mỗi đường => ĐPCM
d, Chứng minh được I O C ^ = 60 0 => ∆ACO đều nên A C D ^ = 30 0
Chứng minh được DCBD đều nên CD = CB => CD = 25cm
Áp dụng tỉ số lượng giác trong ∆CDM ( M ^ = 90 0 ) ta tính được: MD = 12,5cm và MC = 21,7 cm
Từ đó tính được diện tích xung quanh hình trụ tạo thành khi cho tứ giác MCND quay quanh MD là: S x q = 2 r πh = 542 , 5 πcm 2

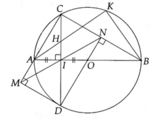
a, H I B ^ = H K B ^ = 180 0
=> Tứ giác BIHK nội tiếp
b, Chứng minh được: DAHI ~ DABK (g.g)
=> AH.AK = AI.AB = R 2 (không đổi)
c, Chứng minh được MCND là hình chữ nhật từ đó => Đpcm

a: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
=>ΔAKB vuông tại K
Xét tứ giác BKHI có
góc BKH+góc BIH=180 độ
=>BKHI là tứ giác nội tiếp
b: Xét ΔAHI vuông tại I và ΔABK vuông tại K có
góc HAI chung
=>ΔAHI đồng dạng với ΔABK
=>AH/AB=AI/AK
=>AH*AK=AI*AB=1/4*R^2

Giải chi tiết:
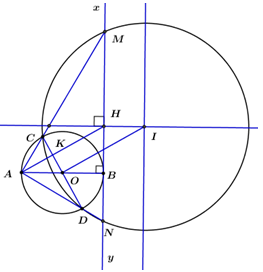
1) Chứng minh tứ giác MCDN nội tiếp.
Xét (O;R)(O;R) ta có: AB,CDAB,CD là hai đường kính của hình tròn
⇒ADBC⇒ADBC là hình bình hành (hai đường chéo cắt nhau tại trung điểm của mỗi đường).
⇒{AC=BDAD=BC⇒{AC=BDAD=BC (các cạnh đối).
Ta có: ∠ADB=900∠ADB=900 (góc nội tiếp chắn nữa đường tròn)
⇒∠BDN=900(1)⇒∠BDN=900(1)
Ta có: ∠CMN∠CMN là góc có đỉnh nằm ngoài đường tròn chắn các cung
BCBC và AB.AB.
⇒∠CMN=12(sdcungAB−sdcungCB)=12sdcungBD=12sdcungAC.(doAC=BD)⇒∠CMN=12(sdcungAB−sdcungCB)=12sdcungBD=12sdcungAC.(doAC=BD)
Lại có: ∠ADC∠ADC là góc nội tiếp chắn cung AC⇒∠ADC=12sdcungACAC⇒∠ADC=12sdcungAC
⇒∠ADC=∠CMN(=12sdcungAC).⇒∠ADC=∠CMN(=12sdcungAC).
⇒CDNM⇒CDNM là tứ giác nội tiếp (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện). (đpcm)
2) Chứng minh AC.AM=AN.AN.AC.AM=AN.AN.
Xét ΔACDΔACD và ΔANMΔANM ta có:
∠CADchung∠AMB=∠ADC(cmt)⇒ΔACD∼ΔANM(g−g)⇒ACAN=ADAM⇒AC.AM=AN.AD(dpcm).∠CADchung∠AMB=∠ADC(cmt)⇒ΔACD∼ΔANM(g−g)⇒ACAN=ADAM⇒AC.AM=AN.AD(dpcm).
3) Gọi I là tâm đường tròn nội tiếp tứ giác MCDN và H là trung điểm MN. Chứng minh tứ giác AOIH là hình bình hành. Khi đường kính CD quay quanh điểm O thì I di động trên đường nào?
Ta có I là tâm đường tròn nội tiếp tứ giác MCDN, H là trung điểm của MN
⇒IH⊥MN⇒IH⊥MN (mối quan hệ giữa đường kính và dây cung).
Mà AO⊥MNAO⊥MN (do AB là đường kính của đường tròn (O), MN là tiếp tuyến tại B của đường tròn)
⇒HI//AO(⊥MN)(1)⇒HI//AO(⊥MN)(1)
Mặt khác ta có ∠CAD=900∠CAD=900 (góc nội tiếp chắn nửa đường tròn)
⇒∠ACD+∠CDA=900⇒∠ACD+∠CDA=900 (tổng hai góc nhọn trong tam giác vuông)
Xét ΔMANΔMAN có ∠MAN=900∠MAN=900, H là trung điểm của MN
⇒AH=12MN=MH⇒AH=12MN=MH (đường trung tuyến ứng với cạnh huyền của tam giác vuông)
⇒ΔAHM⇒ΔAHM cân tại H (dhnb)
⇒∠MAH=∠HMA⇒∠MAH=∠HMA (hai góc kề đáy của tam giác cân).
Lại có : ∠ACD=∠CAB∠ACD=∠CAB (hai góc nội tiếp chắn hai cung AD, CB bằng nhau).
Mà : ∠AMH+∠CAB=900∠AMH+∠CAB=900 (tam giác ABM vuông tại B)
⇒∠MAH+∠ACD=900⇒ΔCAK⇒∠MAH+∠ACD=900⇒ΔCAK vuông tại K⇒CD⊥AH={K}.K⇒CD⊥AH={K}.
Lại có : OI⊥CDOI⊥CD (mối quan hệ giữa đường kính và dây cung)
⇒AH//OI(⊥CD).(2)⇒AH//OI(⊥CD).(2)
Từ (1) và (2) ta có : {AH//OIAO//HI⇒AOIH{AH//OIAO//HI⇒AOIH là hình bình hành (dhnb). (đpcm)
Ta có : HH là trung điểm của MN,M,NMN,M,N thuộc đườn thẳng xyxy cố định ⇒H⇒H là điểm di động trên đường xy.xy.
Vì AOIHAOIH là hình bình hành (cmt) ⇒AO=IH⇒AO=IH (hai cạnh đối)
Mà AO=RAO=R không đổi ⇒IH=R⇒IH=R không đổi.
⇒I⇒I là điểm di động trên đườgn thẳng song song với đường thẳng xy.xy.
4) Khi góc AHB bằng 600; Tính diện tích xung quanh của hình trụ tạo thành khi hình bình hành AHOI quay quanh cạnh AH theo R.
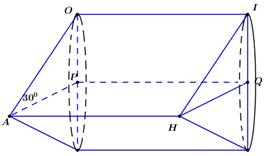
Ta có : ∠AHB=600⇒∠OAH=300∠AHB=600⇒∠OAH=300
Khi quay hình bình hành AHIO một vòng quanh cạnh AH thì cạnh AO và cạnh HI tạo nên hai hình nón bằng nhau có đường sinh AO=IH=R.AO=IH=R.
Cạnh OI tạo nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón cũng như bán kính của hình tròn (O)(O) là R.R.
Gọi P, Q là tâm các đường tròn đáy của hình trụ.
Xét ΔAOPΔAOP ta có : ∠OPA=900,∠OAP=300.∠OPA=900,∠OAP=300.
⇒sin300=OPOA=OPR⇒OP=Rsin300=R2.⇒sin300=OPOA=OPR⇒OP=Rsin300=R2.
Xét ΔABHΔABH ta có : AH=ABtan600=2R√3=2R√33.AH=ABtan600=2R3=2R33.
Diện tích xung quanh hình trụ cần tính là : Sxq=2πrh=2π.OP.AH=2π.R2.2R√33=2πR2√33.

a, Tứ giác BIHK nội tiếp (tổng hai góc đối bằng 180 0 )
b, Chứng minh AH.AK = AI.AB = 1 2 R.2R = R 2 => ĐPCM
c, MCND là hình chữ nhật => MN, AB, CD đồng quy tại I là trung điểm của CD
d, Tam giác OCA đều => A B C ^ = 30 0 ; M C D ^ = 60 0
Tính được CD = 2CI = 2 . 25 2 = 25cm; CM = 25 2 cm, MD = 25 3 2 cm, Sxq = 2.π.CM.MD = 625 3 2 πcm 2