Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé :
1.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM\perp OM,CA\perp OA\)
\(\Rightarrow CAOM\)nội tiếp đường tròn đường kính OC
Tương tự DMOB nội tiếp đường tròn đường kính OD
2 . Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM=CA,OC\) là phân giác \(\widehat{AOM}\)
Tương tự DM = DB , OD là phân giác ^BOM
Mà \(\widehat{AOM}+\widehat{MOB}=180^0\)
\(\Rightarrow OC\perp OD\)
Lại có ; \(OM\perp CD\Rightarrow CM.DM=OM^2\Rightarrow CM.DM=R^2\)
Mà : \(CM=CA,DM=DB\Rightarrow AC.BD=R^2\Rightarrow AC.3R=R^2\Rightarrow AC=\frac{R}{3}\)
\(\Rightarrow S_{ABCD}=\frac{1}{2}AB\left(BD+CA\right)=\frac{1}{2}.2R.\left(3R+\frac{R}{3}\right)=\frac{10R^2}{3}\)
3.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CO\perp AM=E\) là trung điểm AM
Tương tự \(OD\perp BM=F\) là trung điểm BM
\(\Rightarrow MN\) là đường trung bình \(\Delta ABC\Rightarrow EF//MN\)
Mà \(OE\perp ME,OF\perp MF,MN\perp ON\)
\(\Rightarrow M,E,N,O,F\in\) đường tròn đường kính OM
\(\Rightarrow EFNO\) nội tiếp
\(\Rightarrow\widehat{EFO}+\widehat{ENO}=180^0\)
Mà \(\widehat{NEF}+\widehat{ENO}=180^0\) ( EF // AB => EF//NO )
\(\Rightarrow EFON\) là hình thang cân

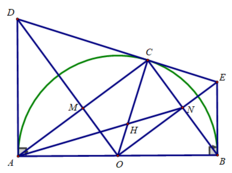
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE

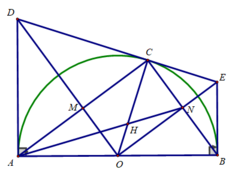
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật

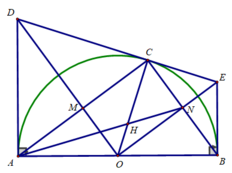
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC 2 = R 2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC 2 = R 2
Khi đó: OM.OD + ON.OE = 2 R 2
Vậy OM.OD + ON.OE không đổi
a) Xét tứ giác AOMC có
\(\widehat{CAO}\) và \(\widehat{CMO}\) là hai góc đối
\(\widehat{CAO}+\widehat{CMO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AOMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Ta có: AOMC là tứ giác nội tiếp(cmt)
nên \(\widehat{MAO}=\widehat{OCM}\)(hai góc cùng nhìn cạnh OM)
hay \(\widehat{MAB}=\widehat{OCD}\)
Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(Gt)
CA là tiếp tuyến có A là tiếp điểm(Gt)
Do đó: OC là tia phân giác của \(\widehat{AOM}\)(Tính chất hai tiếp tuyến cắt nhau)
\(\Leftrightarrow\widehat{AOM}=2\cdot\widehat{COM}\)
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OD là tia phân giác của \(\widehat{MOB}\)(Tính chất hai tiếp tuyến cắt nhau)
\(\Leftrightarrow\widehat{BOM}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{AOM}+\widehat{BOM}=180^0\)(hai góc kề bù)
mà \(\widehat{AOM}=2\cdot\widehat{COM}\)(cmt)
và \(\widehat{BOM}=2\cdot\widehat{MOD}\)(cmt)
nên \(2\cdot\widehat{COM}+2\cdot\widehat{MOD}=180^0\)
\(\Leftrightarrow\widehat{COM}+\widehat{MOD}=90^0\)
mà \(\widehat{COM}+\widehat{MOD}=\widehat{COD}\)(tia OM nằm giữa hai tia OC,OD)
nên \(\widehat{COD}=90^0\)
Xét ΔCOD có \(\widehat{COD}=90^0\)(cmt)
nên ΔCOD vuông tại O(Định nghĩa tam giác vuông)
Xét (O) có
ΔMAB nội tiếp đường tròn(M,A,B∈(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
Xét ΔAMB vuông tại M và ΔCOD vuông tại O có
\(\widehat{MAB}=\widehat{OCD}\)(cmt)
Do đó: ΔAMB∼ΔCOD(g-g)
⇔\(\dfrac{AM}{CO}=\dfrac{BM}{DO}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AM\cdot OD=BM\cdot OC\)(đpcm)