Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

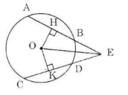
a) Nối OE ta có: AB = CD
=> OH = OK (Định lí 3)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
=> ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)
b) Ta có: OH ⊥ AB
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC. (đpcm)

a)Vì HA=HB nên OH⊥AB
Vì KC=KD nên OK⊥CD
Mặt khác, AB=CD nên OH=OK (hai dây bằng nhau thì cách đều tâm).
ΔHOE=ΔKOE (cạnh huyền, cạnh góc vuông)
Suy ra EH=EK. (1)
b) Ta có AH=KC (một nửa của hai dây bằng nhau). (2)
Từ (1) và (2) suy ra EH+HA=EK+KC hay EA=EC.

a, Ta có : d(O;AB) = OH
d(O;CD) = OK
AB = CD => OH = OK => EB = ED
mà H ; K lần lượt là trung điểm AB và CD => EH = EK
b, Vi OH = OK => AE = EC

Lời giải chi tiết
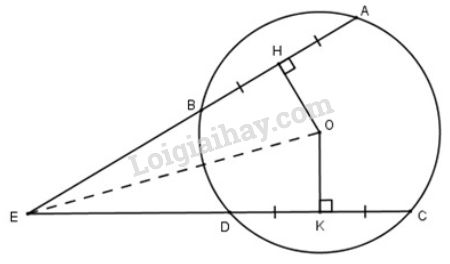
a) Nối OE.
Vì HA=HBHA=HB nên OH⊥ABOH⊥AB (ĐLí 2 - trang 103: đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Vì KC=KDKC=KD nên OK⊥CDOK⊥CD. (ĐLí 2 - trang 103: đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Mặt khác, AB=CDAB=CD nên OH=OKOH=OK (hai dây bằng nhau thì cách đều tâm).
Xét ΔHOEΔHOE và ΔKOEΔKOE có:
OH=OKOH=OK
EOEO chung
ˆEHO=ˆEKO=900EHO^=EKO^=900
Suy ra ΔHOE=ΔKOEΔHOE=ΔKOE (cạnh huyền - cạnh góc vuông)
Suy ra EH=EK(1)EH=EK(1)
b) Theo giả thiết, AB=CDAB=CD nên AB2=CD2AB2=CD2 hay AH=KCAH=KC (2)
Từ (1) và (2) suy ra EH+HA=EK+KCEH+HA=EK+KC
hay EA=EC.
a) Nối OE ta có: AB = CD
=> OH = OK (hai dây bằng nhau thì cách đều tâm)
H là trung điểm của AB nên OH ⊥ AB (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
K là trung điểm của CD nên OK ⊥ CD (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
Do đó ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)
b) Ta có: H là trung điểm của AB nên AH = \(\frac{1}{2}\)AB
K là trung điểm của CD nên CK = \(\frac{1}{2}\)CD
\(AH=\frac{1}{2}AB\)(định lí 1)
Tương tự ta có KC = \(\frac{1}{2}\)CD
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC. (đpcm)

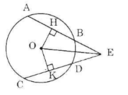
Nối OE ta có: AB = CD
=> OH = OK (Định lí 3)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
=> ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)

A H B E O C K D
a) Nối OE ta có: AB = CD
=> OH = OK (Định lí 3)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
=> \(\Delta OEH=\Delta OEK\)( cạnh huyền, cạnh góc vuông )
=> EH = EK (1). (đpcm)
b) Ta có: \(OH\perp AB\)
\(AH=\frac{1}{2}AB\left(đl1\right)\)
Tương tự , ta có : \(KC=\frac{1}{2}CD\)
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC (đpcm)

Bài tập 13 trang 106 SGK Toán 9 Tập 1 - H7.net
.png)
Câu a: Ta có:
AH=HB⇒OH⊥ABAH=HB⇒OH⊥AB
KC=KD⇒OK⊥CDKC=KD⇒OK⊥CD
Lại có:
AB=CD⇒OH=OKAB=CD⇒OH=OK
⇒ΔHOE=ΔKOE(ch.cgv)⇒ΔHOE=ΔKOE(ch.cgv)
⇒EH=EK(1)⇒EH=EK(1)
Câu b: Ta lại có:
AB=CD⇔AB2=CD2⇔AH=CK(2)AB=CD⇔AB2=CD2⇔AH=CK(2)
Từ (1) và (2):
⇒EH+HA=EK+KC⇔EA=EC
A B C D M K O H
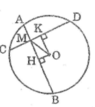
a. Ta có: HA = HB ( gt )
Suy ra : \(OH\perp AB\) ( đường kính dây cung )
Lại có : KC = KD ( gt )
Suy ra : \(OK\perp CD\)( đường kính dây cung )
Mà AB > CD ( gt )
Nên OK > OH ( dây lớn hơn gần tâm hơn )
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
OM2 = OH2 + HM2
Suy ra : HM2 = OM2 – OH2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
OM2 = OK2 + KM2
Suy ra: KM2 = OM2 – OK2 (2)
Mà OH < OK ( cmt ) (3)
Từ (1) (2) và (3) suy ra: HM2 > KM2 hay HM > KM

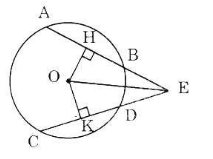
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM
Ta có: OH ⊥ AB
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC. (đpcm)