Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì = 90o (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông MIB có tg
=
=
=>
= 26o34’
Vậy không đổi.
b) Phần thuận:
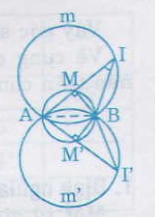
Khi điểm M chuyển động trên đường tròn đường kính AB thì điểm I cũng chuyển động, nhưng luôn nhìn đoạn thẳng AB cố định dưới góc 26o34’, vậy điểm I thuộc hai cung chứa góc 26o34’ dựng trên đoạn thẳng AB (hai cung ![]() và
và ![]() )
)
Phần đảo:
Lấy điểm I' bất kì thuộc ![]() hoặc
hoặc ![]() , I'A cắt đường tròn đường kính AB tại M'.
, I'A cắt đường tròn đường kính AB tại M'.
Tam giác vuông BMT, có tg =
= tg26o34’
Kết luận: Quỹ tích điểm I là hai cung ![]() và
và ![]()
a) Vì \(\widehat{BMA}\)= 90o (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông MIB có tg\(\widehat{AIB}\) = \(\dfrac{MB}{MI}\) = \(\dfrac{1}{2}\) =>\(\widehat{AIB}\) = 26o34’
Vậy \(\widehat{AIB}\) không đổi.
b) Phần thuận:
Khi điểm M chuyển động trên đường tròn đường kính AB thì điểm I cũng chuyển động, nhưng luôn nhìn đoạn thẳng AB cố định dưới góc 26o34’, vậy điểm I thuộc hai cung chứa góc 26o34’ dựng trên đoạn thẳng AB (hai cung ![]() và
và ![]() )
)
Phần đảo:
Lấy điểm I' bất kì thuộc ![]() hoặc
hoặc ![]() , I'A cắt đường tròn đường kính AB tại M'.
, I'A cắt đường tròn đường kính AB tại M'.
Tam giác vuông BMT, có tg\(\widehat{I'}\) = \(\dfrac{M'B}{M'I'}\) = tg26o34’
Kết luận: Quỹ tích điểm I là hai cung ![]() và
và ![]()

a) M ∈ đường tròn đường kính AB
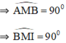
ΔBMI vuông tại M
⇒ tan I = MB / MI = 1/2
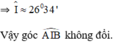
b) Dự đoán: Quỹ tích điểm I là hai cung 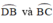 là các cung chứa góc 26º34’ dựng trên đoạn AB.
là các cung chứa góc 26º34’ dựng trên đoạn AB.
Chứng minh:
+ Phần thuận :
Theo phần a): 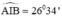 không đổi
không đổi
I nằm trên cung chứa góc 26º34’ dựng trên đoạn AB cố định
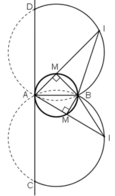
Kẻ tiếp tuyến của đường tròn tại A cắt hai cung chứa góc 26º34’ dựng trên đoạn AB tại C và D
Khi M di động trên đường tròn đường kính AB cố định thì I di động trên cung BC và BD
⇒ I nằm trên hai cung 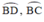 chứa góc 26º34’ dựng trên đoạn AB cố định.
chứa góc 26º34’ dựng trên đoạn AB cố định.
+ Phần đảo:
Lấy điểm I bất kỳ nằm trên hai cung 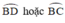 nhìn AB dưới 1 góc 26º34’.
nhìn AB dưới 1 góc 26º34’.
AI cắt đường tròn đường kính AB tại M.

⇒ BM /MI = tan I = 1/2.
Kết luận: Quỹ tích điểm I là hai cung 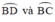 nhìn AB dưới góc 26º34’ (hình vẽ).
nhìn AB dưới góc 26º34’ (hình vẽ).
Kiến thức áp dụng
+ Trong một tam giác vuông, tan α = cạnh đối / cạnh huyền.

Khi điểm M chuyển động trên đường tròn đường kính AB thì điểm I cũng chuyển động, nhưng luôn nhìn đoạn thẳng AB cố định dưới góc 26o34’, vậy điểm I thuộc hai cung chứa góc 26o34’ dựng trên đoạn thẳng AB (hai cung ![]() và
và ![]() )
)
Phần đảo:
Lấy điểm I' bất kì thuộc ![]() hoặc
hoặc ![]() , I'A cắt đường tròn đường kính AB tại M'.
, I'A cắt đường tròn đường kính AB tại M'.
Tam giác vuông BMT, có tg =
= tg26o34’
Kết luận: Quỹ tích điểm I là hai cung ![]() và
và ![]()
Dự đoán: Quỹ tích điểm I là hai cung 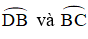
Chứng minh:
+ Phần thuận :
Theo phần a): 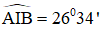
I nằm trên cung chứa góc 26º34’ dựng trên đoạn AB cố định
Kẻ tiếp tuyến của đường tròn tại A cắt hai cung chứa góc 26º34’ dựng trên đoạn AB tại C và D
Khi M di động trên đường tròn đường kính AB cố định thì I di động trên cung BC và BD
⇒ I nằm trên hai cung 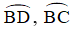
+ Phần đảo:
Lấy điểm I bất kỳ nằm trên hai cung 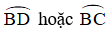
AI cắt đường tròn đường kính AB tại M.
⇒ BM /MI = tan I = 1/2.
Kết luận: Quỹ tích điểm I là hai cung 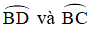

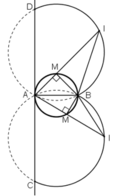
M ∈ đường tròn đường kính AB
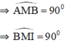
ΔBMI vuông tại M
⇒ tan I = MB / MI = 1/2
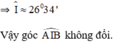

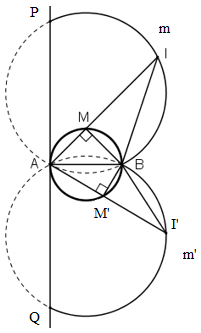
M A B O C
a, có AM = 2AC mà để AM lớn nhất
<=> AC lớn nhất
có AC là dây cung của đường tròn (O) đk AB
=> AC =< AB
dấu = xảy ra khi C trùng B
b, AM = 2R.căn 3 mà AM = 2AC
<=> 2AC = 2R.căn 3
<=> AC = R.căn 3
xét tam giác ABC vuông tại C => AC^2 + CB^2 = AB^2
Mà BA = 2R
=> (R.căn 3)^2 + BC^2 = (2R)^2
<=> 3R^2 + BC^2 = 4R^2
<=> BC^2 = R^2
<=> BC = R
vậy lấy điểm C trên (O) sao cho BC = R để AM = 2R.căn 3
c, xét tam giác BAM có BC là đường trung tuyến đồng thời là đường cao
=> tam giác BAM cân tại B
=> BA = BM mà AB không đổi
=> BM không đổi
=> khi C di động trên (O) thì M di động trên đường tròn (B) cố định

*chứng minh thuận
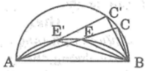
Trong đường tròn đường kính AB ta có:

Khi C chuyển động trên đường tròn đường kính AB cố định thì D chuyển động trên cung chứa góc 135 ° dựng trên đoạn thẳng AB cố định
-Khi dây AC có độ dài lớn nhất bằng đường kính đường tròn thì C trùng với B nên E cũng trùng với B.Vậy B là điểm thuộc quỹ tích
- Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A.khi đó E trùng với A nên A là một điểm của quỹ tích
Vậy E chuyển động trên cung chứa góc 135 ° vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C
*chứng minh đảo:
Lấy điểm E’ bất kì trên cung chứa góc 135 ° , nối AE’ cắt đường tròn đường kính AB tại C’.Nối BE’, BC’

Quỹ tích điểm các điểm E khi C chuyển động trên nửa đường tròn đường kính AB là cung chứa góc 135 ° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C
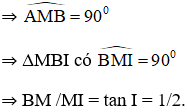


Dự đoán: Quỹ tích điểm I là hai cung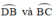 là các cung chứa góc 26º34’ dựng trên đoạn AB.
là các cung chứa góc 26º34’ dựng trên đoạn AB.
Chứng minh:
+ Phần thuận :
Theo phần a):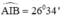 không đổi
không đổi
I nằm trên cung chứa góc 26º34’ dựng trên đoạn AB cố định
Kẻ tiếp tuyến của đường tròn tại A cắt hai cung chứa góc 26º34’ dựng trên đoạn AB tại C và D
Khi M di động trên đường tròn đường kính AB cố định thì I di động trên cung BC và BD
⇒ I nằm trên hai cung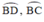 chứa góc 26º34’ dựng trên đoạn AB cố định.
chứa góc 26º34’ dựng trên đoạn AB cố định.
+ Phần đảo:
Lấy điểm I bất kỳ nằm trên hai cung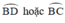 nhìn AB dưới 1 góc 26º34’.
nhìn AB dưới 1 góc 26º34’.
AI cắt đường tròn đường kính AB tại M.
⇒ BM /MI = tan I = 1/2.
Kết luận: Quỹ tích điểm I là hai cung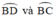 nhìn AB dưới góc 26º34’ (hình vẽ).
nhìn AB dưới góc 26º34’ (hình vẽ).