Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(C\right)\) có tâm \(I\left(3;-1\right)\) và có bán kính \(R=2\), ta có :
\(IA=\sqrt{\left(3-1\right)^2+\left(-1-3\right)^2}=2\sqrt{5}\)
\(IA>R\), vậy A nằm ngoài (C)
b) \(\Delta_1:3x+4y-15=0;\Delta_2:x-1=0\)

a) \(y+1=0\) hay \(15x+8y-112=0\)
b) \(MN=\dfrac{30}{\sqrt{34}}\)

Đường tròn tâm \(I\left(3;-1\right)\) bán kính \(R=\sqrt{3^2+\left(-1\right)^2-6}=2\)
Các đường thẳng gọi hết là d cho dễ kí hiệu
b/ \(\overrightarrow{MI}=\left(2;-4\right)=2\left(1;-2\right)\)
d đi qua M và vuông góc IM nên nhận (1;-2) là 1 vtpt
Pt d: \(1\left(x-1\right)-2\left(y-3\right)=0\Leftrightarrow x-2y+5=0\)
c/ Thay tọa độ N vào đường tròn thỏa mãn \(\Rightarrow N\in\left(C\right)\) \(\Rightarrow IN\perp d\)
\(\overrightarrow{IN}=\left(0;2\right)=2\left(0;1\right)\Rightarrow\) d nhận (0;1) là 1 vtpt và qua N
Pt d: \(0\left(x-3\right)+1\left(y-1\right)=0\Leftrightarrow y-1=0\)
d/ d song song d1 nên pt có dạng: \(5x+12y+c=0\) (với \(c\ne-2019\))
d tiếp xúc (C) nên \(d\left(I;d\right)=R\)
\(\Leftrightarrow\frac{\left|5.3-12.1+c\right|}{\sqrt{5^2+12^2}}=2\Leftrightarrow\left|c+3\right|=26\Rightarrow\left[{}\begin{matrix}c=23\\c=-29\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}5x+12y+23=0\\5x+12y-26=0\end{matrix}\right.\)
e/ Tiếp tuyến vuông góc d2 nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình d có dạng: \(2x-y+c=0\)
d tiếp xúc (C) \(\Rightarrow d\left(I;d\right)=R\)
\(\Leftrightarrow\frac{\left|2.3-1.\left(-1\right)+c\right|}{\sqrt{2^2+1^2}}=2\Leftrightarrow\left|c+7\right|=2\sqrt{5}\Rightarrow\left[{}\begin{matrix}c=-7+2\sqrt{5}\\c=-7-2\sqrt{5}\end{matrix}\right.\)
Có 2 tt thỏa mãn: \(\left[{}\begin{matrix}2x-y-7+2\sqrt{5}=0\\2x-y-7-2\sqrt{5}=0\end{matrix}\right.\)

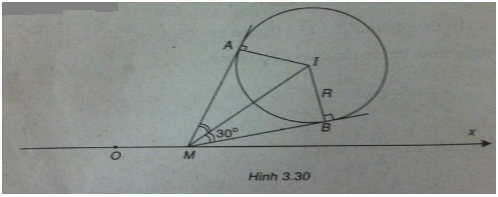
Đường tròn (C) có tâm I (3 ; 3) và có bán kính
\(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {9 + 9 - 14} = 2\)
Điểm M(x;0) thuộc Ox.
Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:
\(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\)
\(\Rightarrow IM = {R \over {\sin {{30}^ \circ }}} = 2R = 4\)
\(IM = 4 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2} + 9} = 4\)
\(\Leftrightarrow {x^2} - 6x + 2 = 0\)
\(\Leftrightarrow x = 3 \pm \sqrt 7\)
Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là :
\({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 - \sqrt 7 ;0} \right)\)





Không phải, bạn chưa học cách viết pttt tại 1 điểm bằng phương pháp "tách đôi tọa độ" à?
Tiếp tuyến của đường tròn (C) có pt: \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\)
tại điểm M nằm trên đường tròn \(M\left(x_M;y_M\right)\) luôn có dạng:
\(\left(x-a\right)\left(x_M-a\right)+\left(x-b\right)\left(x_M-b\right)=R^2\)
Phương trình (C): \(\left(x-3\right)^2+\left(y+1\right)^2=4\)
Đường tròn (C) tâm \(I\left(3;-1\right)\) bán kính \(R=2\)
\(\overrightarrow{AI}=\left(2;-4\right)\Rightarrow AI=2\sqrt{5}\)
Phương trình tiếp tuyến qua \(T_1\) có dạng:
\(\left(x-3\right)\left(x_{T1}-3\right)+\left(y+1\right)\left(y_{T1}+1\right)=4\)
Do tiếp tuyến qua A nên:
\(-2\left(x_{T1}-3\right)+4\left(y_{T1}+1\right)=4\Leftrightarrow x_{T1}-2y_{T1}-3=0\) (1)
Tiếp tuyến qua \(T_2\): \(\left(x-3\right)\left(x_{T2}-3\right)+\left(y+1\right)\left(y_{T2}+1\right)=4\)
Do tiếp tuyến qua A nên:
\(-2\left(x_{T2}-3\right)+4\left(y_{T2}+1\right)=4\Leftrightarrow x_{T2}-2y_{T2}-3=0\) (2)
Từ (1); (2) \(\Rightarrow T_1;T_2\) thuộc đường thẳng có pt: \(x-2y-3=0\)
Gọi H là trung điểm \(T_1T_2\Rightarrow\left\{{}\begin{matrix}IH\perp T_1T_2\\HT_1=HT_2\end{matrix}\right.\)
\(IH=d\left(I;T_1T_2\right)=\frac{\left|3-2\left(-1\right)-3\right|}{\sqrt{1^2+\left(-2\right)^2}}=\frac{2}{\sqrt{5}}\)
\(\Rightarrow HT_1=\sqrt{R^2-IH^2}=\frac{3\sqrt{10}}{5}\Rightarrow T_1T_2=\frac{6\sqrt{10}}{5}\)
\(AH=AI-IH=\frac{8\sqrt{5}}{5}\)
\(S_{AT_1T_2}=\frac{1}{2}AH.T_1T_2=\frac{24\sqrt{2}}{5}\)