Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) x2 + y2 – 4x + 8y – 5 = 0
⇔ (x2 – 4x + 4) + (y2 + 8y + 16) = 25
⇔ (x – 2)2 + (y + 4)2 = 25.
Vậy (C) có tâm I(2 ; –4), bán kính R = 5.
b) Thay tọa độ điểm A vào phương trình đường tròn ta thấy:
(–1 – 2)2 + (0 + 4)2 = 32 + 42 = 52= R2
⇒ A thuộc đường tròn (C)
⇒ tiếp tuyến (d’) cần tìm tiếp xúc với (C) tại A
⇒ (d’) là đường thẳng đi qua A và vuông góc với IA
⇒ (d’) nhận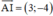 
là một vtpt và đi qua A(–1; 0)
⇒ phương trình (d’): 3(x + 1) – 4(y - 0)= 0 hay 3x – 4y + 3 = 0.
c) Gọi tiếp tuyến vuông góc với (d) : 3x – 4y + 5 = 0 cần tìm là (Δ).
(d) có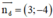 
là một vtpt; 1 VTCP là ud→(4; 3)
(Δ) ⊥ (d) ⇒ (Δ) nhận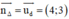 
là một vtpt
⇒ (Δ): 4x + 3y + c = 0.
(C) tiếp xúc với (Δ) ⇒ d(I; Δ) = R
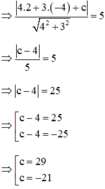
Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.
a) Tâm I(2 ; -4), R = 5
b) Đường tròn có phương trình: (x – 2 )2 + (y + 4)2 = 25
Thế tọa độ A(-1 ; 0) vào vế trái, ta có :
(-1- 2 )2 + (0 + 4)2 = 32 + 42 = 25
Vậy A(-1 ;0) là điểm thuộc đường tròn.
Áp dụng công thức tiếp tuyến (Xem sgk)
Ta được pt tiếp tuyến với đường tròn tai A là:
(-1 – 2)(x – 2) + (0 + 4)(y + 4) = 25 <=> 3x – 4y + 3 = 0
Chú ý:
1. Theo tính chất tiếp tuyến với đường tròn tại 1 điểm thuộc đường tròn thì vuông góc với bán kính đi qua tiếp điểm, ta có thể giải câu này như sau:
Vectơ = (-3; 4)
Tiếp tuyến đi qua A(-1; 0) và nhận làm một vectơ pháp tuyến có phương trình:
-3(x + 1) + 4(y – 0) = 0 ,<=> 3x – 4y + 3 = 0
a.
Ta có: \(\left\{{}\begin{matrix}-4a=-2\\8b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-4\end{matrix}\right.\) \(\Rightarrow I\left(2;-4\right)\)
\(R=\sqrt{2^2+\left(-4\right)^2+5}=5\)
b.
PTTT: \(\left(C\right):\left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0\)
\(\Leftrightarrow\left(2+1\right)\left(x+1\right)+\left(-4-0\right)\left(y-0\right)=0\)
\(\Leftrightarrow\left(C\right):3x-4y=-3\)
c.
Ta có: \(\Delta\perp d\Rightarrow\Delta:4x+3y+c=0\)
\(d\left(I,\Delta\right):\dfrac{\left|4\cdot2-3\cdot4+c\right|}{\sqrt{4^2+3^2}}=5\)
\(\Leftrightarrow\left|c-4\right|=25\) \(\Leftrightarrow\left[{}\begin{matrix}c=29\\c=-21\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\Delta:4x+3y+29=0\\\Delta:4x+3y-21=0\end{matrix}\right.\)
a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:
$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$
Với I là tâm đường tròn, A là điểm trên đường tròn.
Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$
Thay vào công thức ta được:
$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$
Vậy bán kính của đường tròn là $\sqrt{34}$.
Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:
$(x-2)^2 + (y-3)^2 = 34$
b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.
Ta có phương trình đường tròn chính giữa:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Tại điểm M(x,y) trên đường tròn, ta có:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:
$y - y_M = y'(x-x_M)$
Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:
$y + 5 = \frac{-(x-1)}{y+5}(x-1)$
Simplifying:
$x(y+5) + y(x-1) = 6$
Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến
Đề bài thiếu :
Cho đường tròn (C) có phương trình: x2 + y2 - 4x + 8y - 5 = 0
Giải :
a) Tâm I(2 ; -4), R = 5
b) Đường tròn có phương trình: (x - 2 )2 + (y + 4)2 = 25
Thế tọa độ A(-1 ; 0) vào vế trái, ta có :
(-1- 2 )2 + (0 + 4)2 = 32 + 42 = 25
Vậy A(-1 ;0) là điểm thuộc đường tròn.
Áp dụng công thức tiếp tuyến (Xem sgk)
Ta được pt tiếp tuyến với đường tròn tai A là:
(-1 - 2)(x - 2) + (0 + 4)(y + 4) = 25 <=> 3x - 4y + 3 = 0