Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 2 nên
( d ) đi qua A( 2,0 )
Thay A( 2,0 ) vào đường thẳng d ta được
\(\left(1-m\right).2+m+2=0\)
\(2-2m+m+2=0\)
\(4-m=0\)
\(m=4\)
b, Đường thẳng d song song vs đường thẳng y = 2x - 1 nên
1 - m = 0 và m + 2 khác -1
m = 1 và m khác -3

a: Đặt (d1): y=ax+b(a<>0)
Vì (d1) vuông góc với (d) nên 3a=-1
=>\(a=-\dfrac{1}{3}\)
Vậy: (d1): \(y=-\dfrac{1}{3}x+b\)
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x=-b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\dfrac{x}{3}=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3b\\y=0\end{matrix}\right.\)
=>A(3b;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{3}\cdot0+b=b\end{matrix}\right.\)
=>B(0;b)
\(AB=2\sqrt{10}\)
=>\(AB^2=40\)
=>\(\left(0-3b\right)^2+\left(b-0\right)^2=40\)
=>\(10b^2=40\)
=>\(b^2=4\)
=>b=2 hoặc b=-2
Vậy: (d1): y=-1/3x+2 hoặc (d1): y=-1/3x-2
b: Đặt (d2): y=ax+b
Vì (d2)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-5\end{matrix}\right.\)
Vậy: (d2): y=3x+b
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\3x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{b}{3}\end{matrix}\right.\)
=>\(C\left(-\dfrac{b}{3};0\right)\)
tọa độ D là:
\(\left\{{}\begin{matrix}x=0\\y=3x+b=3\cdot0+b=b\end{matrix}\right.\)
=>D(0;b)
\(OC=\sqrt{\left(-\dfrac{b}{3}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{b}{3}\right)^2+0}=\dfrac{\left|b\right|}{3}\)
\(OD=\sqrt{\left(0-0\right)^2+\left(b-0\right)^2}=\sqrt{0^2+b^2}=\left|b\right|\)
Vì Ox\(\perp\)Oy nên OC\(\perp\)OD
=>ΔOCD vuông tại O
=>\(S_{OCD}=\dfrac{1}{2}\cdot OC\cdot OD\)
=>\(S_{OCD}=\dfrac{\dfrac{1}{2}\left|b\right|}{3}\cdot\left|b\right|=\dfrac{1}{2}\cdot\dfrac{b^2}{3}\)
Để \(S_{OCD}=6\) thì \(\dfrac{b^2}{6}=6\)
=>\(b^2=36\)
=>\(b=\pm6\)
Vậy: (d2): y=3x+6 hoặc (d2): y=3x-6
Để ΔOCD cân tại O thì OC=OD
=>\(\dfrac{\left|b\right|}{3}=\left|b\right|\)
=>\(\left|b\right|=0\)
=>b=0
Vậy: (d2): y=3x
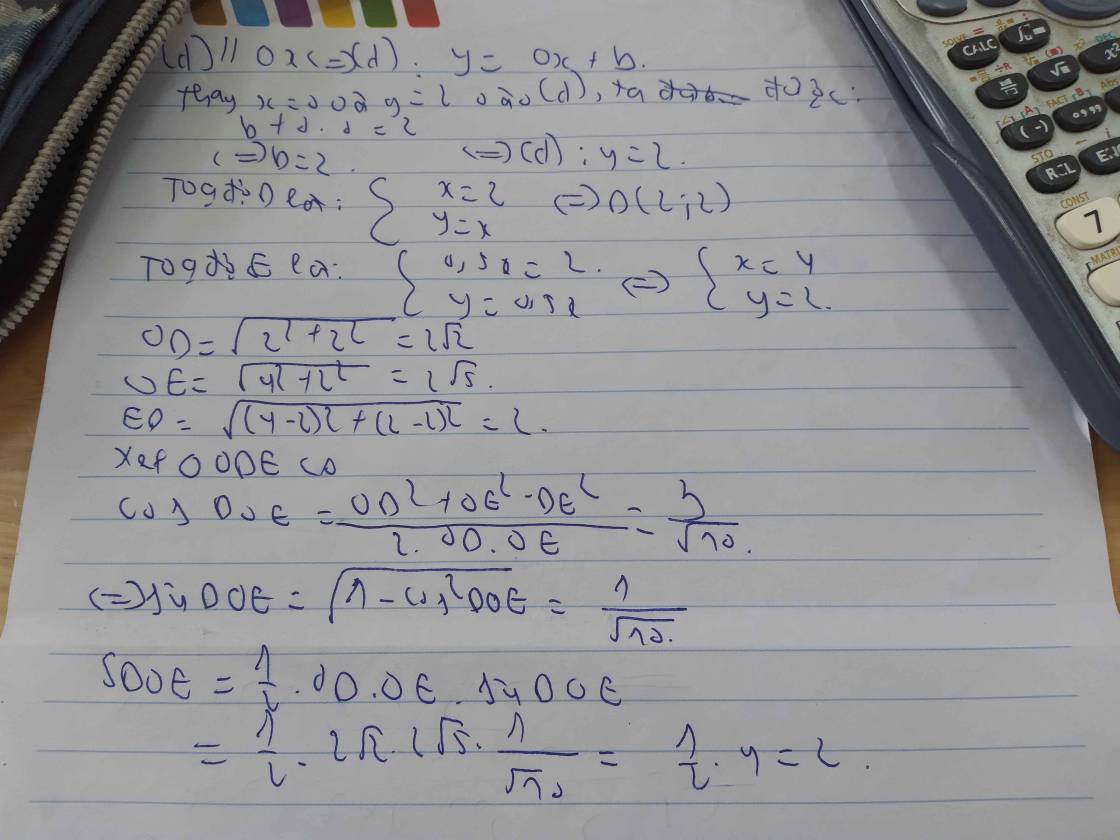
Viết pt đg thẳng (d1) // (d) cắt Ox tại A, Oy tại B và S∆AOB = 8
Gọi (d2) có dạng y = ax + b và (d2) // (d) \(\Rightarrow y=4x+b\)
A có tọa độ = (a;0) \(\Rightarrow O_A=\left|a\right|=4\)
B có tọa độ = (b;0) \(\Rightarrow O_B=\left|b\right|\)
Lại có \(\frac{1}{2}\left|ab\right|=8\Rightarrow\frac{1}{2}.4.\left|b\right|=8\Rightarrow\orbr{\begin{cases}b=4\\b=-4\end{cases}}\)