Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\) Gọi điểm cố định (d) luôn đi qua là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(m-2\right)x_0+2\Leftrightarrow mx_0-2x_0+2-y_0=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=0\\2-2x_0-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=0\\y_0=2\end{matrix}\right.\Leftrightarrow A\left(0;2\right)\)
Vậy \(A\left(0;2\right)\) là điểm cố định mà (d) lun đi qua
\(b,\) PT giao Ox,Oy: \(y=0\Leftrightarrow x=\dfrac{2}{2-m}\Leftrightarrow B\left(\dfrac{2}{2-m};0\right)\Leftrightarrow OB=\dfrac{2}{\left|m-2\right|}\\ x=0\Leftrightarrow y=2\Leftrightarrow C\left(0;2\right)\Leftrightarrow OC=2\)
Gọi H là chân đường cao từ O đến (d) \(\Leftrightarrow OH=1\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=1=\dfrac{1}{OB^2}+\dfrac{1}{OC^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow m^2-4m+4+1=4\\ \Leftrightarrow m^2-4m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2+\sqrt{3}\\m=2-\sqrt{3}\end{matrix}\right.\)
\(c,\) Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OC^2}+\dfrac{1}{OB^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)
Đặt \(OH^2=t\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{m^2-4m+5}{4}\Leftrightarrow t=\dfrac{4}{\left(m-2\right)^2+1}\le\dfrac{4}{0+1}=4\\ \Leftrightarrow OH\le2\\ OH_{max}=2\Leftrightarrow m=2\)

a) Gọi đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=a'x+b'\)
Vì \(\left(d'\right)//\left(d\right)\Rightarrow a'=2\)
Vậy phương trình đường thẳng (d') có dạng \(\left(d'\right):y=2x+b'\)
Mặt khác (d') đi qua M(3;4) nên điểm M(3;4) thuộc \(\left(d'\right):y=2x+b'\)
Thay \(x=3;y=4\)vào hàm số \(y=2x+b'\)ta có:
\(4=2.3+b'\Leftrightarrow b'=-2\)
Vậy phương trình đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=2x-2\)
b) Gọi OH là khoảng cách từ O đến (d). Gọi giao điểm của (d):y = 2x + 6 với hai trục Ox, Oy lần lượt là A(xA;0), B(0;yB).
Thay x = xA; y = 0 vào hàm số y = 2x + 6, ta có: \(0=2x_A+6\Leftrightarrow x_A=-3\)
Thay x = 0; y = yB vào hàm số y = 2x + 6, ta có: \(y_B=2.0+6=6\)
Vì \(OA=\left|x_A\right|;OB=\left|y_B\right|\)\(\Rightarrow OA=\left|-3\right|=3;OB=\left|6\right|=6\)
\(\Delta OAB\)vuông tại O, đường cao OH \(\Rightarrow\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\left(htl\right)\)
Rồi bạn thay OA, OB vào và dễ dàng tính được OH

a:Thay x=-2 và y=0 vào (d), ta được:
-2(m-1)+4=0
=>-2(m-1)=-4
=>m-1=2
=>m=3
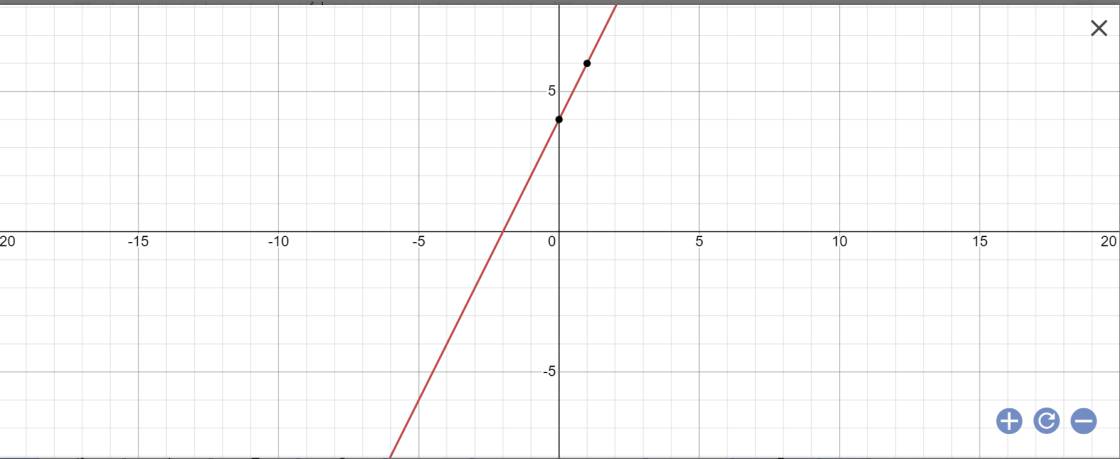
b: (d): y=2x+4

Lời giải:
Nếu $m-1=0$ thì $(d): y=2$
Khoảng cách từ $O$ đến đường thằng $y=2$ là $2$
Nếu $m-1\neq 0$
Gọi $A,B$ lần lượt là giao của $(d)$ với trục hoành và trục tung.
$y_A=0\Rightarrow x_A=\frac{y_A-2m}{m-1}=\frac{-2m}{m-1}$
$x_B=0\Rightarrow y_B=(m-1)x_B+2m=2m$
$\Rightarrow OA=|x_A|=|\frac{2m}{m-1}|; OB=|y_B|=|2m|$
Gọi khoảng cách từ $O$ đến $(d)$ là $h$ thì theo công thức hệ thức lượng trong tam giác vuông tại có:
$\frac{1}{h^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{(m-1)^2}{(2m)^2}+\frac{1}{(2m)^2}=\frac{m^2-2m+2}{4m^2}$
$\Rightarrow h=\frac{2|m|}{\sqrt{m^2-2m+2}}$
Tổng kết 2 TH ta thấy khoảng cách từ $O$ đến $(d)$ là $h=\frac{2|m|}{\sqrt{m^2-2m+2}}$

y = kx +3 <=>kx+3-y=0 => x=0,y=3
đường thẳng d luôn đi qua một điểm cố định(0;3)
b)khoảgn cách từ gốc toạ độ O tới đường thẳng d bằng căn 2 của x^2+y^2
=>x^2+y^2=4 (1)
Thế y = kx +3, \(x^2+\left(kx+3\right)^2=4\)
\(x^2\left(1+k^2\right)+6kx+5=0\)có nghiệm khi k>=\(\frac{\sqrt{5}}{3}\)
c)
Gọi A và B lần lượt là giao điểm của d với Ox và Oy
\(\Rightarrow A\left(-2;0\right)\) và \(B\left(0;2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA=\left|x_A\right|=2\\OB=\left|y_B\right|=2\end{matrix}\right.\)
\(\Rightarrow\Delta OAB\) vuông cân tại O
Gọi H là hình chiếu vuông góc của O lên d \(\Rightarrow OH=d\left(O;d\right)\)
Mặt khác do OAB vuông cân \(\Rightarrow\) OH là đường cao đồng thời là trung tuyến
\(\Rightarrow OH=\dfrac{1}{2}BC=\dfrac{1}{2}\sqrt{OA^2+OB^2}=\sqrt{2}\)
cho đường thẳng (d) : y=X+2 khoảng cách từ gốc tọa độ đến đường thẳng (d) là