Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách làm:
B1: NHÌN KĨ VÀO SGK MỤC TỪ VUÔNG GÓC ĐẾN SONG SONG LÀ LÀM ĐƯỢC BÀI A
B2: LẬT LẠI MỤC TÍNH CHẤT HAI ĐƯƠNG THẲNG SONG SONG ĐỂ GIẢI BÀI B
ĐÃ XONG! THANKS
x' y' x y m n 60 độ N C M D
a) Ta có: \(xy\perp mn\) và \(x'y'\perp mn\)
\(\implies xy//x'y'\)
Vậy xy//x'y'(đpcm)
b) Ta có: \(xy//x'y'\) (câu a)
\(\implies \widehat{MCD}+\widehat{NDC}=180^0\) ( 2 góc trong cùng phía)
\(\implies 60^0+\widehat{NDC}=180^0\)
\(\implies \widehat{NDC}=180^0-60^0=120^0\)
Vậy góc NDC=120 độ.
_Học tốt_

a, xét \(\Delta\)BEM và \(\Delta\)CFM có:
\(\widehat{B}\)=\(\widehat{C}\)(gt)
BM=CM(trung tuyến AM)
\(\Rightarrow\)\(\Delta\)BEM=\(\Delta\)CFM(CH-GN)
b,Ta có \(\Delta\)ABM=\(\Delta\)ACM(c.c.c)
\(\Rightarrow\)\(\widehat{BAM}\)=\(\widehat{CAM}\)
Gọi O là giao của AM và EF
xét tam giác OAE và tam giác OAF có:
AO cạnh chung
\(\widehat{OAE}\)=\(\widehat{OAF}\)(cmt)
vì AB=AC mà EB=FC nên AE=AF
\(\Rightarrow\)tam giác OAE=tam giác OAF(c.g.c)
\(\Rightarrow\)\(\widehat{AOE}\)=\(\widehat{AOF}\)mà 2 góc này ở vị trí kề bù nên\(\widehat{AOE}\)=\(\widehat{AOF}\)=90 độ(1)
\(\Rightarrow\)OE=OF suy ra O là trung điểm EF(2)
từ (1) và (2) suy ra AM là đg trung trực của EF
c, vì \(\widehat{BAM}\)=\(\widehat{CAM}\)=> AM là p/g của \(\widehat{BAC}\)(1)
ta có tam giác BAM=tam giác CAM(c.g.c)
=> AD là p/g của góc BAC(2)
từ (1) và(2) suy ra AM và AD trùng nhau nên A,M,D thẳng hàng
a, Ta có : Tam giác ABC cân tại A => Góc B=Góc C
Xét tam giác BEM vuông tại E và tam giác CFM vuông tại F
BM=CM (BM là trung tuyến)
Góc B=Góc C
=> Tam giác BEM=Tam giác CFM(ch-gn)
b,Từ a, \(\Delta\)BEM=\(\Delta CFM\)=> ME=MF (1);BE=FC
Mà AB=AC=> AE=AF(2)
Từ 1 và 2 => AM là trung trực của EF

a) CM
Xét DBEM và DCFM, có:
E=F=90 Độ
MB=MC(AM là đường trung tuyến)
B =C (DABC cân tại A)
Suy ra : DBEM=DCFM(Cạnh huyền-góc nhọn)

(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
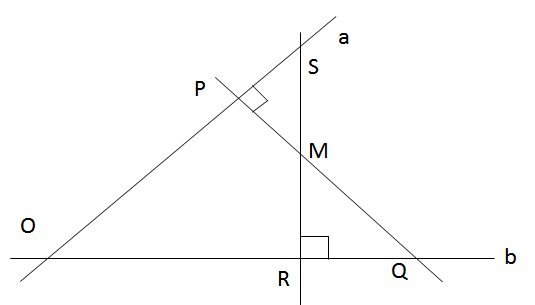
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b