Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Kẻ CO cắt BD tại E
Xét ΔOAC vuông tại A và ΔOBE vuông tại B có
OA=OB
góc COA=góc EOB
Do đó: ΔOAC=ΔOBE
=>OC=OE
Xét ΔDCE có
DO vừa là đường cao, vừalà trung tuyến
nên ΔDEC cân tại D
=>góc DCE=góc DEC=góc CAO
=>CO là phân giác của góc DCA
Kẻ CH vuông góc với CD
Xét ΔCAO vuông tại A và ΔCHO vuông tại H có
CO chung
góc ACO=góc HCO
DO đó: ΔCAO=ΔCHO
=>OA=OH=OB và CH=CA
Xét ΔOHD vuông tại H và ΔOBD vuông tại B có
OD chung
OH=OB
Do đó: ΔOHD=ΔOBD
=>DH=DB
=>AC+BD=CD
b: Gọi M là trung điểm của CD
Xét hình thang ABDC có
O,M lần lượt là trung điểm của AB,CD
nên OM la đường trung bình
=>OM//AC//BD
=>OM vuông góc với AB
=>CD là tiếp tuyến của (O)
c: AC*BD=CH*HD=OH^2=R^2=AB^2/4

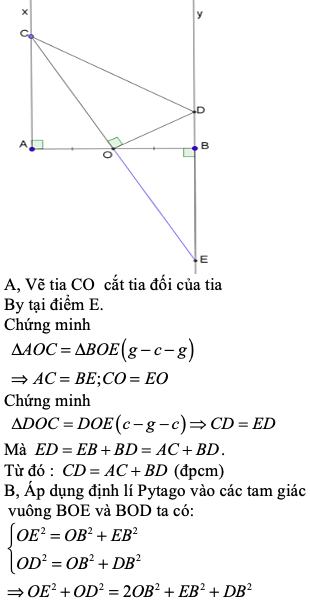
a) Vẽ tia CO cắt tia đối của tia By tại E
Xét tam giác vuông AOC và tam giác vuông BOE có :
AO = OB ( gt )
AOC = BOE ( 2 góc đối đỉnh )
\(\implies\) tam giác vuông AOC = tam giác vuông BOE ( cạnh huyền - góc nhọn )
\(\implies\) AC = BE ( 2 cạnh tương ứng )
Xét tam giác vuông DOC và tam giác vuông DOE có :
OD chung
OC = OE ( tam giác vuông AOC = tam giác vuông BOE )
\(\implies\) tam giác vuông DOC = tam giác vuông DOE ( 2 cạnh góc vuông )
\(\implies\) CD = ED ( 2 cạnh tương ứng )
Mà ED = EB + BD
\(\implies\) ED = AC + BD
\(\implies\) CD = AC + BD
c) Xét tam giác DOE vuông tại O có :
OE2 + OD2 = DE2 ( Theo định lý Py - ta - go )
Xét tam giác BOE vuông tại B có :
OB2 + BE2 = OE2 ( Theo định lý Py - ta - go ) ( * )
Xét tam giác BOD vuông tại B có :
OB2 + BD2 = OD2 ( Theo định lý Py - ta - go ) ( ** )
Cộng ( * ) với ( ** ) vế với vế ta được :
OE2 + OD2 = 2. OB2 + EB2 + DB2
Mà OE2 + OD2 = DE2 ( cmt )
\(\implies\) DE2 = 2. OB2 + EB2 + DB2
= 2. OB2 + EB . ( DE - BD ) + DB . ( DE - BE )
= 2. OB2 + EB . DE - EB . BD + DB . DE - DB . BE
= 2. OB2 + ( EB . DE + DB . DE ) - 2 . BD . BE
= 2. OB2 + DE . ( EB + DB ) - 2 . BD . BE
= 2. OB2 + DE2 - 2 . BD . BE
\(\implies\) 2. OB2 - 2 . BD . BE = 0
\(\implies\) 2. OB2 = 2 . BD . BE
\(\implies\) OB2 = BD . BE
Mà BE = AC ( cmt ) ; OB = AB / 2 ( gt )
\(\implies\) AC . BD = ( AB / 2 )2
\(\implies\) AC . BD = AB2 / 4

a, Xét tam giác DOB và tam giác IOA ta có :
^DOB = ^IOA ( đối đỉnh )
^AIO = ^ODB ( DB // CA do cùng vuông AB và 2 góc này ở vị trí so le trong )
^OAI = ^OBD = 900
Vậy tam giác DOB = tam giác IOA ( ch - gn )
=> OD = OI ( 2 góc tương ứng )
b, Xét tam giác ICD có CO vuông ID hay CO là đường cao
Lại có IO = OD ( cmt ) => CO là đường trung tuyến
=> tam giác ICD cân tại C => CI = CD (2)
Mặt khác : tam giác DOB = tam giác IOA ( cmt ) => BD = IA (1)
=> CI = AC + IA lại có (1) ; (2) => CD = AC + BD
c, Dựng OH vuông CD
Xét tam giác DHO và tam giác HBO ta có :
^DHO = ^HBO = 900
^HDO = ^ODB ( cùng ''='' ^CID )
OD _ chung
Vậy tam giác DHO = tam giác HBO ( g.c.g )
=> OH = OB = R
Vậy CD là tiếp tuyến đường tròn (O)
a)Gọi I là trung điểm của CD
Xét hình thang ACDB (AC//BD) có:\(\hept{\begin{cases}CI=ID\\AO=BO\end{cases}}\)
=>OI là đường tung bình của hình thang ACDB
=>\(OI=\frac{AC+BD}{2}=\frac{CD}{2}=CI=DI\)
=>Tam giác COD vuông tại O
=> đpcm
b)Kẻ OE vuông góc với CD,giao cuae CO và BD là F
Ta có tam giác ACO=Tam giác BFO( cạnh góc vuông-góc nhọn kề)
=>OC=OF
Xét tam giác CDF có:
CO=OF (cmt)
DO vuông góc với CF
=>tam giác CDF cân tại D
=>DO là phân giác góc CDF
=>góc EDO=BDO
=>tam giác EOD=tam giác BOD(Cạnh huyền - góc nhọn)
=>OE=OB
=>EO là bán kính (O) mà OE vuông góc với BC(cách vẽ)
=>CD là tiếp tuyến đường tròn đường kính AB