Question

[wary reus]

Cho đoạn thẳng AB và điểm C nằm giữa 2 điểm A và B người ta kẻ trên nửa mặt phẳng bờ AB 2 tia Ax , By vuông góc với AB. Trên tia Ax lấy điểm I . Tia vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính CI cắt IK tại P

a, C/M: AI.BK=AC.CB

b, C/M: Tam giác ABP vuông

c, Cho A, B ,I cố định. Xác định vị trí C sao cho diện tích ABKI lớn nhất

Answer 1

[Trần Quang Đài]

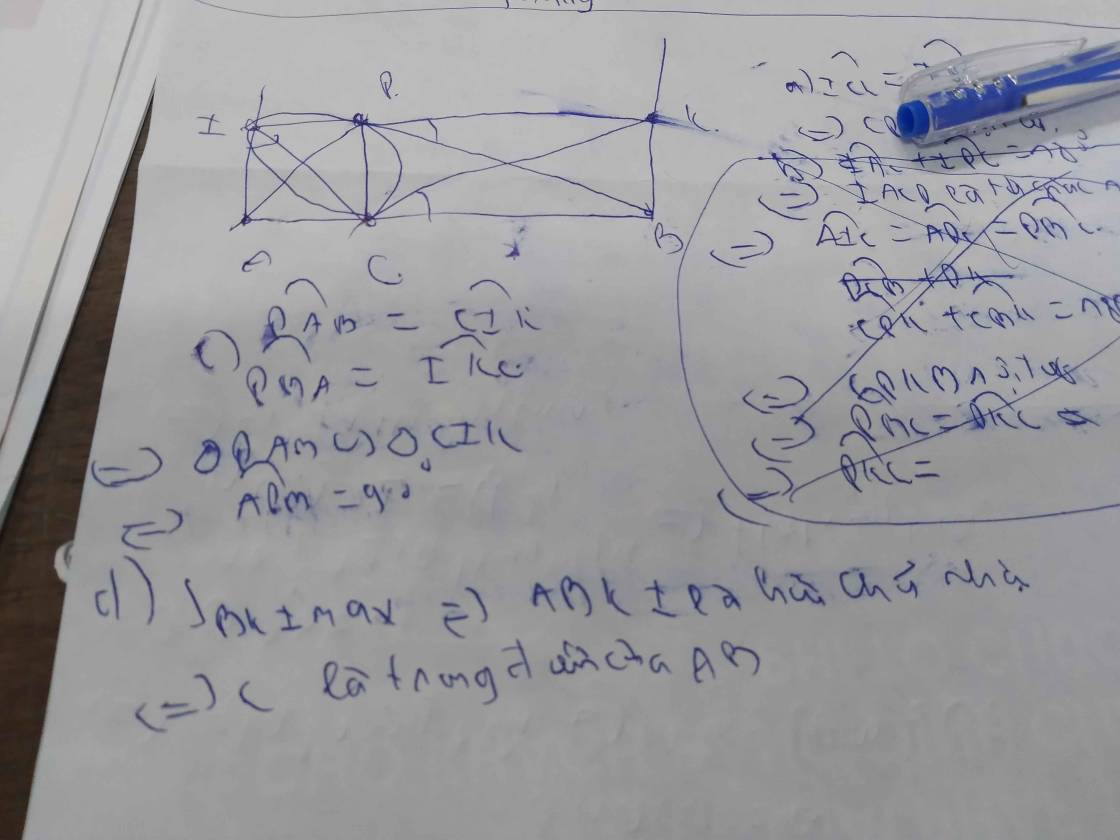
a,Xét \(\Delta AIC\) và \(\Delta BCK\) có :

\(\widehat{AIC}=\widehat{BCK}\) (cùng phụ với \(\widehat{ICA}\) )

\(\widehat{IAC}=\widehat{CBK}\) (=\(90\))

Do đó \(\Delta AIC\infty\Delta BCK\) (g-g)

suy ra \(\dfrac{AI}{AC}=\dfrac{CB}{BK}\)

suy ra đpcm

b,

Ta có \(\widehat{ICP}=90\) (góc nt chắn nửa đường tròn )

suy ra tứ giác CPKB nội tiếp 1 đường tròn

suy ra \(\widehat{CPB}\) =\(\widehat{CKB}\) (góc nt cùng chắn cung CD)

mà \(\widehat{CKB}=\widehat{ICA}\) (do 2 tam giác đồng dạng ở câu a)

Nên \(\widehat{CPB}=\widehat{ICA}\)

Ta có \(\widehat{APB}=\widehat{APC}+\widehat{CPB}=\widehat{APC}+\widehat{ICA}=\dfrac{1}{2}\left(sđAI+sđAC\right)\)

Mà \(\widehat{AOI}=sđAI;\widehat{AOC}=sđAC\)

suy ra \(\dfrac{1}{2}\left(sđAI+sđAC\right)=\dfrac{1}{2}\left(\widehat{AOI}+\widehat{AOC}\right)=\dfrac{1}{2}.180=90\)

Do đó \(\widehat{APB}=90\)

suy ra tam giác ABP vông tại P

c,\(S_{ABKI}=\dfrac{AB\left(KB+AI\right)}{2}\)

Mà AB,AI cố định nên để \(S_{ABKI}\) lớn nhất buộc BK lớn nhất

Ta có \(\Delta AIC\infty\Delta BCK\) (câu a)

\(\Rightarrow\dfrac{BK}{BC}=\dfrac{AC}{AI}\)

\(\Rightarrow BK=\dfrac{AC.BC}{AI}\le\dfrac{\left(AC+BC\right)^2}{4AI}=\dfrac{AB^2}{4AI}\)

Dấu = xảy ra khi và chỉ khi AC=BC

suy ra C là trung điểm của AB

(cái chỗ sử dụng bất đẳng thức theo ab=<(a+b)^2 /4 với mọi a,b là các số không âm )