Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn tự vẽ hình nha
a,Ta có E đối xứng vs c qua d
-> D là trung điểm EC
Xét tứ giác EBCA có
DB=DA=1/2 AB( D là trung điểm BA-gt)
DE=DC=1/2EC( D là trung điểm EC-cmt)
mà EC cắt BA tại D
-> EBCA là hình bình hành( tứ giác có hai đg chéo cắt nhau tại trung điểm mỗi đg)
-> EB=AC và EB song song AC
b, Ta có HA=AC( H đối C qua A-gt)
mà EB=AC(Cmt), EB song song AC(cmt)
-> HA = EB; HA song song EB
Xét tứ giác EBAH có
HA=EB( cmt)
HA song song EB(cmt)
-> EBHA là hình bình hành( 1 cặp đối song song và bằng nhau)
Ta lại có ,góc BAC +góc BAH= 180 độ( kề bù)
mà góc BAC=90 độ( tam giác ABC vuong tại A-gt)
-> góc BAH= 90 độ
Ta có EBAH là hình bình hành(cmt)
mà góc BAH=90 độ(cmt)
-> EBAH là hcn( Hình bình hành có 1 góc vuông)

a: D đối xứng với M qua AB
nên DM vuông góc với AB tại trung điểm của DM
=>E là trung điểm của DM và AB là phân giác của góc DAM(2)
=>AD=AM; BD=BM
mà DA=DB
nên AD=AM=BD=BM
D đối xứng với N qua AC
nên AC vuông góc với DN tại trung điểm của DN
=>AC là phân giác của góc NAD(1) và F là trung điểm của DN
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nên AEDF là hình chữ nhật
b: Từ (1), (2) suy ra góc MAN=2*90=180 độ
=>M,A,N thẳng hàng
mà AM=AN
nên A là trung điểm của MN
c: Để AEDF là hình vuông thì AD là phân giác của góc FAE
mà AD là trung tuyến ứng với BC
nên ΔABC cân tại A
=>AB=AC

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

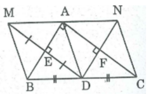
Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng qua điểm A.

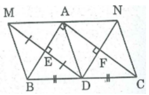
Điểm M và điểm D đối xứng qua trục AB
Suy ra AB là đường trung trực của đoạn thẳng MD
⇒ AB ⊥ DM ⇒ ∠ (AED) = 90 0
Điểm D và điểm N đối xứng qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN ⇒ AC ⊥ DN ⇒ ∠ (AFD) = 90 0
Mà ∠ (EAF) = 90 0 (gt). Vậy tứ giác AEDF là hình chữ nhật (vì có 3 góc vuông).

Gọi O là giao điểm của AC và DN
Vì N và D đối xứng nhau qua AC
nên AC là đường trung trực của DN
=>AC vuông góc với DN tại trung điểm của DN
hay O là trung điểm của DN
Xét ΔABC có
D là trung điểm của BC
DO//AB
Do đó: O là trung điểm của AC
Xét tứ giác ADCN có
O là trung điểm của AC
O là trung điểm của DN
Do đó: ADCN là hình bình hành
mà DA=DC
nên ADCN là hình thoi