Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

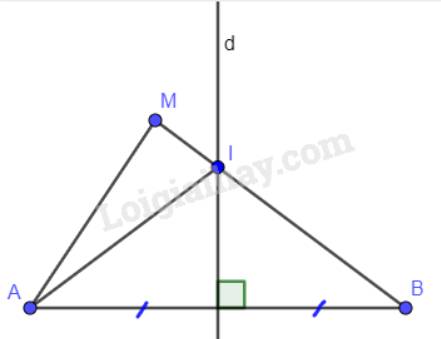
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).

a. M là trung điểm của AN => AM = MN
N là trung điểm của MB => MN = NB
=> AM = MN = NB
Ta có AB = AM + MN + NB
=> AB = 3MN
b. I là trung điểm của MN => MI = IN
Ta có AI = AM + MI
BI = BN + IN
Mà AM = BN (theo câu a)
IM = IN (cmt)
=> AI = BI
=> I là trung điểm của AB
Chúc bạn học tốt!

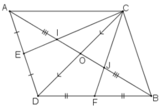
Gọi O là giao điểm của hai đoạn thẳng AB và CD.
⇒ AO = OB và CO = OD.
+ ΔACD có trung tuyến AO, CE cắt nhau tại I
⇒ I là trọng tâm ΔACD
⇒ AI = 2/3. AO = 2/3. 1/2. AB = 1/3.AB
+ Tương tự J là trọng tâm ΔBCD
⇒ BJ = 2/3. BO = 2/3. 1/2. BA = 1/3.AB
⇒ IJ = AB – AI – BJ = 1/3.AB
Vậy AI = IJ = JB

Đường thẳng xy là đường trung trực của đoạn thẳng AB thì:
A. Đường thẳng xy vuông góc với đoạn thẳng AB tại I và I là trung điểm của đoạn AB.
B. Đường thẳng xy vuông góc với đoạn thẳng AB.
C. Đường thẳng xy đi qua trung điểm của đoạn thẳng AB
D. Đường thẳng xy vuông góc với đoạn thẳng AB tại A .

Lời giải:
Do $I$ là trung điểm của $AB$ nên $IA=\frac{1}{2}AB=\frac{1}{2}.20=10$ (cm)