Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công suất tiệu thụ cực đại của mạch P m a x = U 2 2 R 0 ⇒ U 2 = P m a x 2 R = 9600 .
→ Công suất tiêu thụ khi R = 18 Ω là P = U 2 R R 2 + Z L − Z C 2 = U 2 R R 2 + R 0 2 = 192 W.
Đáp án C

Đáp án A
+ Ta có:
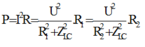
Thay R1 = 125 W và R2 = 150 W vào phương trình trên ta tìm được
![]()
+ 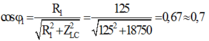
+ 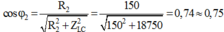

Đáp án D
+ Công suất tiêu thụ của mạch

→ Hai giá trị của R cho cùng công suất thỏa mãn
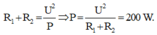

Khi dung kháng là $100 \Omega$ thì công suất tiêu thụ của đoạn mạch là cực đại bằng 100 W nên
\(\begin{cases} Z_L=Z_{C_1}=100 \Omega \\ P=\dfrac{U^2}{R} =100 W \end{cases}\)
Khi dung kháng là $200 \Omega$ thì điện áp hiệu dụng giữa hai đầu tụ điện là $100\sqrt{2} V$ nên
$U_{C_2}=\dfrac{U.Z_{C_2}}{Z}=\dfrac{200.U}{\sqrt{R^2+(100-200)^2}}=100\sqrt{2}$
$\Rightarrow 2U^2=R^2+100^2$
$\Rightarrow 2.100.R =R^2 +100^2$
$\Rightarrow R=100 \Omega$

Ta có P 1 = P 6 → giá trị của R cho công suất cực đại là R 0 = R 1 R 6 = 24 Ω
Với R 3 gần R 0 nhất → P 3 lớn nhất.
Đán án C
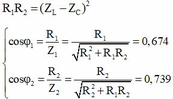


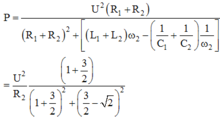


Đáp án B
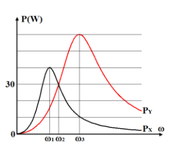
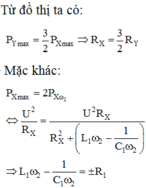
+ Ta có:
+ Khi R thay đổi để Pmax thì: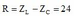 Ω tương ứng với công suất
Ω tương ứng với công suất