Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vecto của hiệu điện thế hai đầu mạch bằng tổng hai vecto hiệu điện thế của động cơ điện và cuộn dây
Vẽ giản đồ vecto ta có thể tổng hợp và tính độ lớn của hiệu điện thế hai đầu mạch
Dùng phép chiếu tính các giá trị theo thành phần thẳng đứng và nằm ngang
\(U_x=U\cos15+2U\cos75\)
\(U_y=U\sin15+2U\sin75\)
\(U=\sqrt{U^2_x+U^2_y}=U\sqrt{7}\)

khi w=wo trong mạch xảy ra cộng hưởng ,cường độ dòng điện hiêu dụng là I max,còn khi w=w1 hoặc w=w2 thì dòng điện trong mạch có cùng giá trị hiệu dụng
nên \(\omega_0^2=\omega_1\omega_2=\frac{1}{LC}\Rightarrow\omega_2L=\frac{1}{\omega_1C}\Rightarrow Z_{L2}=Z_{C1}\)
\(I_{max}=\frac{U}{R}\)
\(I=\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{C1}\right)^2}}=\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{L2}\right)^2}}\)
Theo giả thiết: \(I=\frac{I_{max}}{\sqrt{5}}\)
\(\Rightarrow\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{L2}\right)^2}}=\frac{U}{\sqrt{5}R}\Rightarrow R^2+\left(Z_{L1}-Z_{L2}\right)^2=5R^2\)
\(\Rightarrow\left|Z_{L1}-Z_{L2}\right|=2R\)
\(\Rightarrow L\left(\omega_2-\omega_1\right)=2R\Rightarrow\frac{1}{\pi}.150\pi=2R\Rightarrow R=75\Omega\)
Đáp án B.

Khi ω = ω1 thì dòng điện sớm pha hơn điện áp một góc 30°
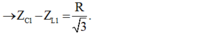
- Ta chú ý rằng là hai giá trị của tần số góc cho cùng giá trị hiệu dụng của dòng điện trong mạch.
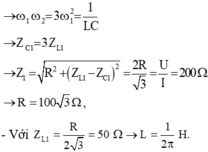

Đáp án C
+ Khi ω = ω1 thì dòng điện sớm pha hơn điện áp một góc 30 0 → Z C 1 - Z L 1 = R 3
+ Ta chú ý rằng là hai giá trị của tần số góc cho cùng giá trị hiệu dụng của dòng điện trong mạch.
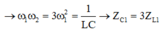
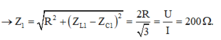

=> 1 2 π H

Mình hướng dẫn thế này để bạn tự tính nhé.
a. \(\omega\) thay đổi để UR max khi hiện tượng cộng hưởng xảy ra \(\Rightarrow\omega=\frac{1}{\sqrt{LC}}\)
b. \(\omega\) thay đổi để UL max khi \(\omega=\frac{1}{X.C}\), với \(X=\sqrt{\frac{L}{C}-\frac{R^2}{2}}\)
c. \(\omega\) thay đổi để Uc max khi \(\omega=\frac{X}{L}\) với X ở câu b.

Khi C = C1 để Uc max thì:
\(Z_{C1}=\frac{R^2+Z_L^2}{Z_L}\) (1)
và \(U_{Cmax}=U\frac{\sqrt{R^2+Z_L^2}}{R}\)(2)
Khi C2 = 2,5C1 thì \(Z_{C2}=\frac{Z_{C1}}{2,5}=0,4Z_{C1}\)
Do i trễ pha hơn u nên: \(Z_L>\frac{Z_C}{2,5}\)
Theo đề bài: \(\tan\frac{\pi}{4}=\frac{Z_L-0,4Z_{C1}}{R}=1\Rightarrow R=Z_L-0,4Z_{C1}\)(3)
Thay vào (1): \(Z_{C1}.Z_L=R^2+Z_L^2=\left(Z_L-0,4Z_{C1}\right)+Z_L^2\Rightarrow2Z_L^2-1,8Z_{C1}Z_L+0,16Z_{C1}^2=0\)
\(\Rightarrow Z_L=0,8Z_{C1}\) hoặc \(Z_L=0,1Z_{C1}\)(loại)
Thay vào (3) \(\Rightarrow R=0,5Z_L\)
Thay vào (2) \(\Rightarrow U_{Cmax}=\frac{U\sqrt{Z_L^2+0,25Z_L^2}}{0,5Z_L}=100\sqrt{5}\Rightarrow U=100V\)
Đáp án B.
