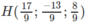Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đường thẳng ∆ có vectơ chỉ phương →uu→(1 ; 2 ; 1). H ∈ ∆ nên H(2 + t ; 1 + 2t ; t).
Điểm H ∈ ∆ là hình chiếu vuông góc của A lên ∆ khi và chỉ khi −−→AHAH→ ⊥ →uu→.
Ta có −−→AHAH→(1+t ; 1 + 2t ; t) nên:
−−→AHAH→ ⊥ →uu→ ⇔ →u.−−→AHu→.AH→ = 0.
⇔ 1 + t + 2(1 + 2t) + t = 0
⇔ 6t + 3 = 0 ⇔ t = −12−12.
⇔ H(32;0;−12)H(32;0;−12).
b) Gọi A' là điểm đối xứng của A qua ∆ và H là hình chiếu vuông góc của A lên ∆ thì H là trung điểm của AA'; vì vậy tọa độ của H là trung bình cộng các tọa độ tương ứng của A và A'.
Gọi A'(x ; y ; z) ta có:
x+12=32x+12=32 => x = 2; y = 0; z = -1.
Vậy A'(2 ; 0 ; -1).

a) Gọi \(\overrightarrow{u}\left(1;-2;-1\right)\) là vectơ chỉ phương của d, giả sử \(\overrightarrow{v}\left(a;b;c\right)\) là 

a) Ta có : \(y'=3x^2+2\left(m-1\right)x+m\left(m-3\right)\)
Hàm số (1) có cực đại và cực tiểu nằm 2 phía đối với trục tung <=> phương trình : \(3x^2+2\left(m-1\right)x+m\left(m-3\right)=0\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow P< 0\Leftrightarrow m\left(m-3\right)< 0\Leftrightarrow0< m< 3\)
Vậy \(0< m< 3\) là giá trị cần tìm
b) Khi m = 1 ta có : \(y=x^3-2x\).
Gọi \(M\left(a;a^3-2a\right)\in\left(C\right),a\ne0\)
Ta có \(y'=3x^2-2\) nên hệ số góc của \(\Delta\) là \(y'\left(a\right)=3a^2-2\)
Ta có \(\overrightarrow{OM}\left(a;a^3-2a\right)\) nên hệ số góc đường thẳng OM là \(k=a^2-2\)
Do đó : \(\Delta\perp OM\Leftrightarrow y'_a.k=-1\)
\(\Leftrightarrow\left(3a^2-2\right)\left(a^2-2\right)=-1\Leftrightarrow3a^4-8a^2+5=0\)
\(M_1\left(1;-1\right);M_1\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a^2=1\\a^2=\frac{5}{3}\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a=\pm1\\a=\pm\frac{\sqrt{5}}{3}\end{array}\right.\)(Thỏa mãn)
Suy ra có 4 điểm thỏa mãn đề bài :\(M_1\left(1;-1\right);M_2\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\)

Do điểm H thuộc d nên \(H\left(1-t;2t;-3+3t\right)\).
\(\overrightarrow{IH}=\left(4-t;-2+2t-2+3t\right)\)
Đường thẳng d có vectơ chỉ phương \(\overrightarrow{u}=\left(-1;2;3\right)\)
Do H là hình chiếu của I trên đường thẳng d nên:
\(\overrightarrow{IH}\perp\overrightarrow{u}\Rightarrow\overrightarrow{IH}.\overrightarrow{u}=\overrightarrow{0}\\ \Leftrightarrow-4+t-4+4t-6+9t=0\\ \Leftrightarrow14t-14=0\\ \Leftrightarrow t=1\)
Suy ra \(H\left(3;0;1\right)\)

Cho H(2+t;1+2t;t) ∈ ∆ . Ta có: A H → =(1+t;1+2t;t) đường thẳng ∆ có vecto chỉ phương a → =(1;2;1). Vì H là hình chiếu vuông góc của A trên ∆ nên AH vuông góc với ∆ <=> A H → . a → = 0
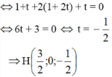

Câu 28:
\(\overrightarrow{CB}=\left(1;-1;1\right)\)
Do (P) vuông góc BC nên nhận (1;-1;1) là 1 vtpt
Phương trình (P):
\(1\left(x-1\right)-1\left(y-1\right)+1\left(z+5\right)=0\)
\(\Leftrightarrow x-y+z+5=0\)
Câu 29:
Mạt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên nhận các vecto có dạng \(\left(k;-2k;3k\right)\) cũng là các vtpt với \(k\ne0\)
Do đó đáp án B đúng (ko tồn tại k thỏa mãn)
Với đáp án A thì \(k=-2\) , đáp án C thì \(k=3\), đáp án D có \(k=1\)





Phương trình tham số của ∆ :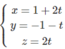
Xét điểm H(1 + 2t; −1 − t; 2t) ∈ ∆
Ta có MH → = (2t − 1; −t; 2t − 1)
a ∆ → = (2; −1; 2)
H là hình chiếu vuông góc của M trên ∆ ⇔ MH → . a ∆ → = 0
⇔ 2(2t − 1) + t + 2(2t − 1) = 0 ⇔ t = 4/9
Ta suy ra tọa độ điểm