Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có
ΔNDP nội tiếp đường tròn(N,D,P∈(O))
NP là đường kính của (O)(gt)
Do đó: ΔNDP vuông tại D(Định lí)
⇒ND⊥DP tại D
hay ND⊥MP(đpcm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔNMP vuông tại N có ND là đường cao ứng với cạnh huyền MP, ta được:
\(MN^2=MD\cdot MP\)(đpcm)
b) Vì N,E∈(O) và N,O,E không thẳng hàng
nên NE là dây của (O)
Xét (O) có
OM là một phần đường kính
NE là dây(cmt)
OM⊥NE tại H(gt)
Do đó: H là trung điểm của NE(Định lí đường kính vuông góc với dây)(đpcm)

a) MN là tiếp tuyến đường tròn (O) \(\Rightarrow\widehat{MNP}=90^o\)
DO = ON = OP => \(DO=\frac{1}{2}NP\Rightarrow\widehat{NDP}=90^o\)
- Aps dụng hệ thức lượng cho tam giác MNP vuông tại N đường cao ND , ta có :
MN2 = MD . MP ( đpcm )
b) Ta có : PE // OM => PE // OH
Mà O là trung điểm của NP => OH là đường trung bình của tam giác ENP
=> H là trung điểm NE
Vậy : HN = HE ( đpcm )
c) Theo ( c/m câu b ) : HN = HE => \(HE\perp OM\)
Áp dung hệ thức trong tam giác NMO vuông tại N , đường cao NH :
Ta có : ON2 = OM . OH => OP2 = OM . OH
\(\Rightarrow\frac{OP}{OM}=\frac{OH}{OP}\left(1\right)\)
- Xét 2 tam giác: OHP và OPM
có : \(\frac{OP}{OM}=\frac{OH}{OP}\left(theo\left(1\right)\right)\)
\(\widehat{O}\)là góc chung
Do đó : \(\Delta OHP~\Delta OPM\left(c-g-c\right)\)
\(\Rightarrow\widehat{OPH}=\widehat{OMP}\left(đpcm\right)\)

a. Em tự giải
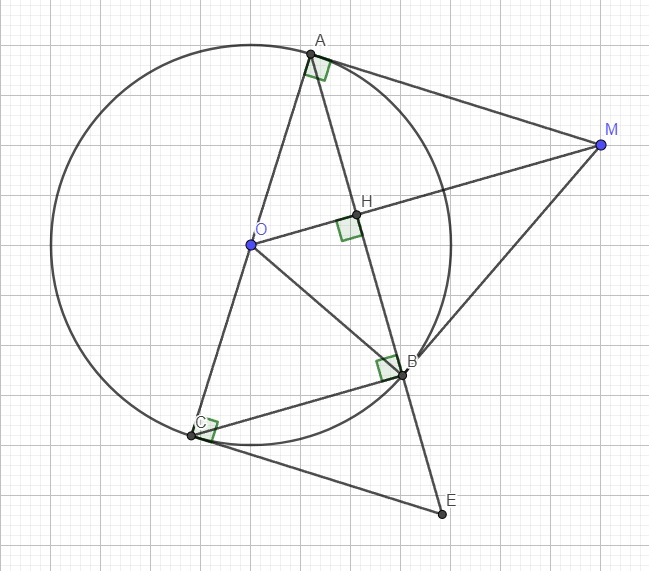
b.
\(\Delta OAB\) cân tại O (do \(OA=OB=R\), mà \(OH\) là đường vuông góc (do OH vuông góc AB)
\(\Rightarrow OH\) đồng thời là trung tuyến và trung trực của AB
Hay OM là trung trực của AB
\(\Rightarrow MA=MB\Rightarrow\Delta MAB\) cân tại M
c.
Do EC là tiếp tuyến tại C \(\Rightarrow EC\perp AC\)
MA là tiếp tuyến tại A \(\Rightarrow MA\perp AC\)
\(\Rightarrow EC||MA\Rightarrow\widehat{MAH}=\widehat{CEB}\) (so le trong)
Mà \(\widehat{MAH}=\widehat{MOA}\) (cùng phụ \(\widehat{AMH}\))
\(\Rightarrow\widehat{CEB}=\widehat{MOA}\)
Xét hai tam giác CEB và MOA có:
\(\left\{{}\begin{matrix}\widehat{CEB}=\widehat{MOA}\left(cmt\right)\\\widehat{CBE}=\widehat{MAO}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta CEB\sim\Delta MOA\left(g.g\right)\)
\(\Rightarrow\dfrac{BE}{OA}=\dfrac{BC}{AM}\Rightarrow BE.AM=BC.OA\)
Mà \(MA=MB\) (theo cm câu b) và \(OA=BO=R\)
\(\Rightarrow BE.BM=BC.BO\)

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO\(\perp\)AB

2: góc OME+góc OAE=180 độ
=>OMEA nội tiếp
=>góc AOE=góc AME=góc OMB

a) Xét (O) có
ΔNDP nội tiếp đường tròn(N,D,P∈(O))
NP là đường kính của (O)(gt)
Do đó: ΔNDP vuông tại D(Định lí)
⇒ND⊥DP tại D
hay ND⊥MP(đpcm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔNMP vuông tại N có ND là đường cao ứng với cạnh huyền MP, ta được:
MN2=MD⋅MPMN2=MD⋅MP(đpcm)
b) Vì N,E∈(O) và N,O,E không thẳng hàng
nên NE là dây của (O)
Xét (O) có
OM là một phần đường kính
NE là dây(cmt)
OM⊥NE tại H(gt)
Do đó: H là trung điểm của NE(Định lí đường kính vuông góc với dây)(đpcm)

Hình vẽ:
a, \(AH\perp MC\Rightarrow AH=HD\)
Ta có \(\left\{{}\begin{matrix}OA=OD\\HA=HD\end{matrix}\right.\Rightarrow OM\) là trung trực của \(AD\)
\(\Rightarrow MA=MD\Rightarrow\Delta OAM=\Delta ODM\left(c-c-c\right)\)
\(\Rightarrow MD\perp OD\)
Hay MD là tiếp tuyến
b, \(\Delta OAM\) vuông tại A
\(\Rightarrow O;A;M\) thuộc đường tròn đường kính OM
Lại có \(\Delta ODM\) vuông tại D
\(\Rightarrow O;D;M\) thuộc đường tròn đường kính OM
Dễ chứng minh được B là trung điểm OM
\(\Rightarrow M;A;O;D\in\left(B;R\right)\)
c, Vì \(\widehat{BAC}=90^o\Rightarrow\Delta BAC\) vuông tại A
\(\Rightarrow HB.HC=HA^2\)
Mà \(\Delta OAM\) vuông tại A \(\Rightarrow HM.HO=HA^2\)
\(\Rightarrow HB.HC=HM.HO\)